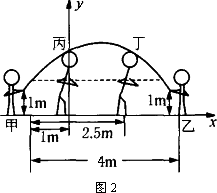
平时我们在跳大绳时，绳甩到最高处的形状可近似地看为抛物线，如图1所示，正在甩绳的甲、乙两名学生拿绳的手间距为4 m，距地面均为1 m，学生丙、丁分别站在距甲拿绳的手水平距离1 m、2.5 m处，绳子在甩到最高处时刚好通过他们的头顶，已知学生丙的身高是1.5 m，则学生丁的身高为多少？(建立的平面直角坐标系如图2所示)

启明公司生产某种产品，每件产品成本是3元，售价是4元，年销售量为10万件．为了获得更好的效益，公司准备拿出一定资金做广告．根据经验，每年投入的广告赞是x(万元)时，产品的年销售量将是原销售量的y倍，且y＝－x²＋x＋，如果把利润看作是销售总额减去成本费和广告费．

(1)试写出年利润S(万元)与广告费x(万元)的函数关系式，并计算出广告费是多少万元时，公司获得的年利润最大，最大的年利润是多少万元？

(2)把(1)中的最大利润留出3万元做广告，其余的资金投资新项目，现有6个项目可供选择，各项目每股投资金额与预计收益如下表：

如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，问有几种符合要求的投资方式？写出每种投资方式所选的项目．

如图，矩形ABCD中，AB＝3，BC＝4，线段EF在对角线AC上，EG⊥AD，FH⊥BC，垂足分别是G、H，且EG＋FH＝EF．

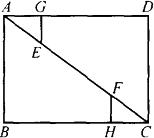
(1)求线段EF的长；

(2)设EG＝x，△AGE与△CFH的面积和为S，写出S关于x的函数关系式及自变量x的取值范围，并求出S的最小值．

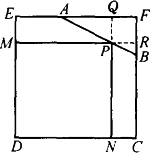
如图，已知边长为4的正方形，截去一角成五边形ABCDE，其中AF＝2，FB＝1，在AB上求一点P，使矩形PNDM有最大面积，并求出这个最大面积．

用三种不同的方法解方程x－－3＝0．

如果方程x²＋(m－1)x＋(m－3)＝0的一根大于1且小于2，另一根小于1，求m的取值范围．

已知二次函数y＝－x²＋bx＋c，且不等式－x²＋bx＋c＞0的解集是－5＜x＜－1．

(1)求这个二次函数的解析式；

(2)这个二次函数的图象，经过怎样的平移，可使它与x轴只有一个交点？

(3)这个二次函数的图象，经过怎样的平移，满足当x＜0时，y随着x的增大而增大；当x＞0时，y随着x的增大而减小？

(4)试写出同时满足(2)、(3)的函数解析式．

如果方程x²＋(m－2)x＋(5－m)＝0有一根大于2，小于3，另一根比3大，求实数m的范围．

某医药研究所进行某一新药的开发，经过大量的服用试验后可知：成年人按规定的剂量服用后，每毫升血液中含药量y(μg)(1μg＝10^－3 mg)随时间x(h)的变化规律与某一个二次函数y＝ax²＋bx＋c(a≠0)相吻合，并测得服用时(即时间为0时)每毫升血液中含药量为0μg；服用后2 h每毫升血液中含药量为6μg；服用后3 h每毫升血液中含药量为7.5μg．

(1)试求出含药量y(μg)与服药时间x(h)的函数解析式，并画出0≤x≤8内的函数图象的示意图；

(2)求服药后几小时，才能使每毫升血液中含药量最大，并求出血液中的最大含药量；

(3)结合图象说明一次服药后的有效时间是多少小时．(有效时间为血液中含药量大于或等于μg的总时间)

如图，设A、B为二次函数y＝－3x²－2x＋m的图象与x轴的两个交点，P为抛物线的顶点，当△PAB为等腰直角三角形时，求二次函数的函数关系式．