某校九年级的一场篮球比赛中，如图所示，队员甲正在投篮，已知球出手时离地面高m，与篮圈中心的水平距离为7 m，当球出手后水平距离为4 m时到达最大高度4 m．设篮球的运动轨迹为抛物线，篮圈距地面3 m．

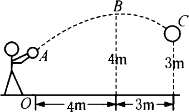
(1)请你建立适当的平面直角坐标系，并判定此球能否准确投中？

(2)此时，若对方队员乙在甲面前1 m处跳起盖帽拦截，已知乙的最大摸高为2.9 m，那么他能否获得成功？

阅读理解题．

阅读材料：当抛物线的解析式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发生变化．

例如：由抛物线y＝x²－2mx＋m²＋2m－1，　　①

有y＝(x－m)²＋2m－1．　　　　　　　　　　②

∴抛物线的顶点坐标为(m，2m－1)，

即

当m的值变化时，x、y的值也随之变化，因而y值也随x值的变化而变化．

将③代入④，得y＝2x－1．　　　　　　　　　⑤

可见，不论m取任何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式：y＝2x－1．

解答问题：

(1)在上述过程中，由①到②所用的数学方法是________，其中运用了________公式；

由③、④得到⑤所用的数学方法是________．

(2)根据阅读材料提供的方法，确定抛物线y＝x²－2mx＋2m²－3m＋1顶点的纵坐标y横坐标x之间的关系式．

已知抛物线y＝ax²＋bx＋c经过A(1，－4)、B(－1，0)、C(－2，5)三点．

(1)求抛物线的解析式并画出这条抛物线；

(2)直角坐标系中，点的横坐标与纵坐标均为整数的点称为整点．试结合图象，写出在第四象限内抛物线上的所有整点的坐标．

某旅游胜地欲开发一座景观山．从山的侧面进行勘测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位：百米)．已知AB所在抛物线的解析式为y＝－x²＋8，BC所在抛物线的解析式为y＝(x－8)²，且已知B(m，4)．

(1)设P(x，y)是山坡线AB上任意一点，用y表示x，并求点B的坐标；

(2)从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20 cm，长度因坡度的大小而定，但不得小于20 cm，每级台阶的两端点在坡面上(如上图)．

①分别求出前三级台阶的长度(精确到1 cm)；

②这种台阶不能一起铺到山脚，为什么？(可取点验证)

(3)在山坡上的700 m高度(点D)处恰好有一小块平地，可以用来建造索道站．索道站的起点选择在山脚水平线上的点E处，OE＝1 600(m)．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y＝(x－16)²．试求索道的最大悬空高度．

某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支(不含进价)总计120万元．在销售过程中发现，年销售量y(万件)与销售单价x(元)之间存在着如图1所示的一次函数关系．

(1)求y关于x的函数关系式；

(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利＝年销售额－年销售产品总进价－年总开支)．当销售单价x为何值时，年获利最大？并求这个最大值；

(3)若公司希望该种产品一年的销售获利不低于40万元，借助图2中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？

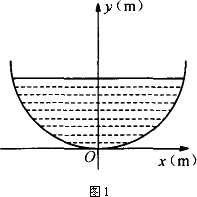
公园要建圆形的喷水池(如图1)，在水池中央垂直于水面安装一个柱子OA，O恰好在水面中心，OA＝1.25 m，由柱子顶端A处的喷头向外喷水，水流在各个方面沿形状相同的抛物线路线落下．为使水流形状较为漂亮，要求设计成水流在与OA距离1 m处达到距水面最大高度2.25 m．如果不计其他因素，那么水池半径至少要多少米，才能使喷出的水流不致落到水池外？

某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程．如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．

根据图提供的信息，解答下列问题：

(1)由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；

(2)截止到几月末公司累积利润可达到30万元？

(3)第8个月公司所获利润是多少万元？

如图(1)是某段河床横断面的示意图．查阅该河段的水文资料，得到下表中的数据：

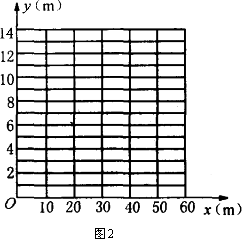
(1)请你以上表中的各对数据(x，y)作为点的坐标，尝试在图(2)所示的坐标系中画出y关于x的函数图象；

(2)①填写下表：

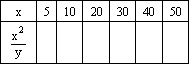
②根据所填表中数据呈现的规律，猜想出用x表示y的二次函数表达式：__________；

(3)当水面宽度为36 m时，一艘吃水深度(船底部到水面的距离)为1.8 m的货船能否在这个河段安全通过？为什么？

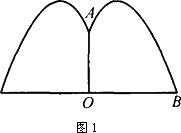
一副眼镜的两镜片下半部分轮廓线可以近似看成抛物线形状．建立如图所示的平面直角坐标系．已知左轮廓线端点A、B间的距离为4 cm，点A、B与右轮廓线端点D、E均在平行于x轴的直线上，最低点C在x轴上，且与AB的距离CH＝1 cm，y轴平分BD，BD＝2 cm，解答下列问题：

(1)求轮廓线ACB所对应的二次函数关系式(写出自变量x的取值范围)；

(2)由(1)写出右轮廓线DFE的函数关系式及自变量x的取值范围．

如图1是泰州某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1 m，拱桥的跨度为10 m，桥洞与水面的最大距离是5 m，桥洞两侧壁上各有一盏距离水面4 m的景观灯．若把拱桥的截面图放在平面直角坐标系中(如图2)．

(1)求抛物线的解析式．

(2)求两盏景观灯之间的水平距离．