
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出x的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少元?
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
已知△ABC中,AD是BC边上的高,AD与AB的夹角为锐角α,AB=15,tan∠ACD=![]() .又x1,x2是关于x的方程8x2-4x-2cosα+1=0的两个实根,并且满足32(
.又x1,x2是关于x的方程8x2-4x-2cosα+1=0的两个实根,并且满足32(![]() +
+![]() )=
)=![]() .
.
(1)求cosα的值.
(2)求S△ABC的值.
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
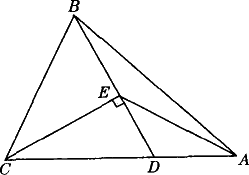
如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE.
(1)写出图中所有相等的线段,并加以证明;
(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;
(3)求△BEC与△BEA的面积之比.
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
已知如图(1),在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的异侧,BD⊥AE,CE⊥AE,垂足分别为D、E.(1)求证:BD=DE+CE.(2)若直线AE绕点A旋转到图(2)位置(BD<CE),其余条件不变,猜想BD与DE、CE的关系,并给出证明.(3)若直线AE绕点A旋转到图(3)位置(BD>CE),其余条件不变,再猜想BD与DE、CE的关系(直接写出结果,不必证明).(4)归纳(1)、(2)、(3),请用简洁语言表达BD、DE、CE的关系.
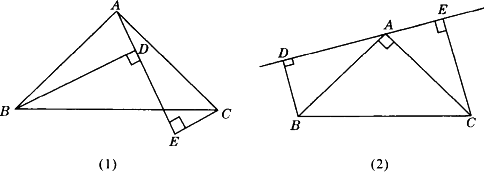
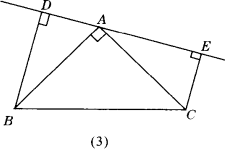
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图,M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON.
(1)求图(1)中∠MON的度数;
(2)图(2)中∠MON的度数是________,图(3)中∠MON的度数是________.
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).

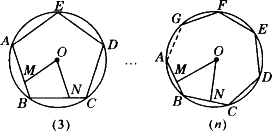
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图,在△ABC中,点E、F在BC边上,点D、G分别在AB、AC边上,四边形DEFG是矩形,若矩形DEFG的面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K.
求![]() 的值.
的值.
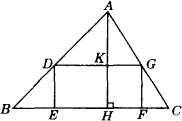
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=3,BC=1.连结BF,分别交AC、DC、DE于点P、
Q、R.
(1)求证:△BGF∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答(根据提出问题的层次和解答过程评分).
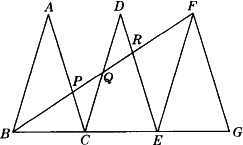
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
一块直角三角形木板的一条直角边AB长为1.5米,面积为1.5米2,要把它加工成一个面积最大的正方形桌面.甲、乙两位同学的加工方法如图所示,请你用学过的知识说明哪位同学的加工方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
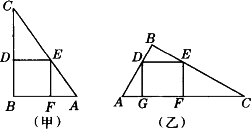
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图,在四边形ABCD中,AC=6,BD=8且AC⊥BD,顺次连结四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连结四边形A1B1C1D1各边中点得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn.

(1)证明:四边形A1B1C1D1是矩形;
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积;
(3)写出四边形AnBnCnDn的面积;
(4)求四边形A5B5C5D5的周长.
查看答案和解析>>
科目: 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图,已知∠MON=90°,等边三角形ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为一边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证:△ACQ∽△AB1D;
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com