
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
某公园草坪的护栏是由50段形状相同的抛物线形组成的,为牢固起见,每段护栏需按间距0.4 m加设不锈钢管作为的立柱(如图).为了计算所需不锈钢立柱的总长度,设计人员利用图所示的坐标系进行计算.(1)求该抛物线的解析式;
(2)计算所需不锈钢管立柱的总长度.

查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
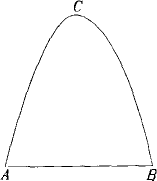
某工厂大门是一抛物线形水泥建筑物(如下图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
如图(a)所示,有一块铁皮,拱形边缘呈抛物线状,MN=4分米,抛物线顶点处到边MN的距离是4分米.要在铁皮下截下一矩形ABCD,使矩形顶点B,C落在边MN上,A,D落在抛物线上,问这样截下的矩形铁皮的周长能否等于8分米?(提示:以MN所在的直线为x轴建立适当的直角坐标系)

查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.(1)一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触上绳子.求绳子最低点到地面的距离;(2)为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳长正好各为2米,木板与地面平行.求此时木板到地面的距离(供选用数据:![]() ≈1.8,
≈1.8,![]() ≈1.9,
≈1.9,![]() ≈2.1).
≈2.1).

查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
如图所示,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴,拱桥的DG![]() 部分为一段抛物线,顶点G的高度为8米,AD和A
部分为一段抛物线,顶点G的高度为8米,AD和A![]() 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和![]() 为两个方向的汽车通行区,宽都为15米,线段CD和C
为两个方向的汽车通行区,宽都为15米,线段CD和C![]() 为两段对称的上桥斜坡,其坡度为1∶4.
为两段对称的上桥斜坡,其坡度为1∶4.
(1)求桥拱DG![]() 所在抛物线的解析式及C
所在抛物线的解析式及C![]() 的长;
的长;
(2)求BE和![]() 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和![]() 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和![]() 的宽.
的宽.
(3)按规定,汽车通行该桥下时载货最高处和桥拱之间的距离不得小于0.4米.今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米.它能否从OA(或![]() )区域安全通过?请说明理由.
)区域安全通过?请说明理由.
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
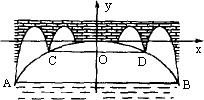
如图,有一座抛物线型的拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.(1)在如图的坐标系中求抛物线的解析式.(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
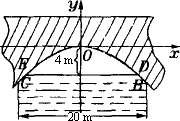
有一座抛物线形拱桥,正常水位时桥下水面宽度为20 m,拱顶距离水面4 m,(1)在如图所示的直角坐标系中,求出该抛物线的解析式;(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出将d表示为h的函数解析式;(3)设正常水位时桥下的水深为2 m,为保证过往船只顺利航行,桥下水面宽度不得小于18 m.求:水深超过多少米时,就会影响过往船只在桥下顺利航行.
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
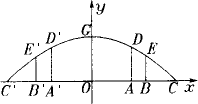
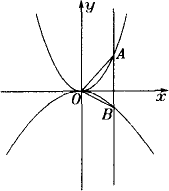
如图,两条抛物线y=x2,y=-![]() x2和直线x=a(a>0)分别交于A、B两点,已知∠AOB=90°,(1)求通过O点,把△AOB的面积两等分的直线解析式;(2)为使直线y=
x2和直线x=a(a>0)分别交于A、B两点,已知∠AOB=90°,(1)求通过O点,把△AOB的面积两等分的直线解析式;(2)为使直线y=![]() x+b与线段AB相交,那么b应在怎样的范围才合适?
x+b与线段AB相交,那么b应在怎样的范围才合适?
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
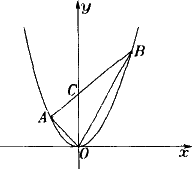
已知抛物线y=x2和直线y=(m2-1)x+m2.(1)当m为何实数时,抛物线与直线有两个交点?(2)设坐标原点为O,抛物线与直线的交点从左到右分别为A、B.如下图所示,当直线与抛物线两交点的横坐标之差为3时,求△AOB中OB边上的高.
查看答案和解析>>
科目: 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
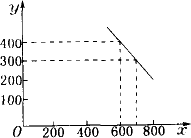
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(如图下所示).
(1)根据图象,求一次函数y=kx+b的表达式;(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试用销售单位x表示毛利润S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com