某房地产公司要在一块如图所示的矩形小区ABCD中，规划建造一个小区公园(矩形GHCK)，为了使文物保护区(△AEF)不受破坏，矩形公园的顶点G不能在文物保护区内，已知AB＝200 m，AD＝160 m，AE＝60 m，AF＝40 m．

(1)当矩形小区公园的顶点G恰好是EF的中点时，求公园的面积；

(2)当G在EF上什么位置时，公园面积最大？

某商店经销一种销售成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量下降10千克．

(1)当销售单价定为每千克55元时，计算月销售量和月销售利润；

(2)设销售单价为每千克x元，月销售利润为y元，求y与x之间的函数关系式；

(3)若利润达到8千元，问单价定为多少元(月销售成本不得超过1万元)？

某公司推出一种高效环保洗涤用品，年初上市后，公司经历了从亏损到赢利的过程，下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．

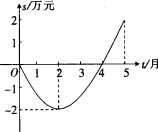
(1)求累积利润s(万元)与销售时间t(月)之间的函数关系式；

(2)求截止到几月末公司累积的利润可达到30万元；

(3)求第8个月公司所获利润是多少万元？

如下图，表示近5年来某市的财政收入情况，图中x轴上的1，2，…，5依次表示第1年，第2年，…，第5年，即2002年，2003年，…，2006年．可以看出，图中的折线近似于抛物线的一部分．

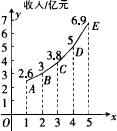
(1)请你求出过A，C，D三点的二次函数的解析式；

(2)分别求当x＝2和x＝5时(1)中二次函数的函数值；并分别与B，E两点的纵坐标相比较；

(3)利用(1)中的二次函数的解析式预测2007年该市的财政收入．

利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理)．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出1吨建筑材料共需支付厂家及其他费用100元．设每吨材料售价为x(元)，该经销店的月利润为y(元)．

(1)当每吨售价是240元时，计算此时的月销售量；

(2)求出y与x的二次函数关系式(不要求写出x的取值范围)；

(3)请把(2)中的二次函数配方成y＝a(x－h)²＋k的形式，并据此说明，该经销店要获得最大月利润，售价应定为每吨多少元；

(4)小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．

如下图所示，点O是坐标原点，点A(n，0)是x轴上一动点(n＜0)．以AO为一边作矩形AOBC，使OB＝2OA，点C在第二象限．将矩形AOBC绕点A逆时针旋转90°得矩形AGDE．过点A的直线y＝kx＋m(k≠0)交y轴于点F，FB＝FA．抛物线y＝ax²＋bx＋c过点E，F，G且和直线AF交于点H，过点H作x轴的垂线，垂足为点M．

(1)求k的值；

(2)点A位置改变时，△AMH的面积和矩形AOBC的面积比是否改变？说明你的理由．

我市英山县某茶厂种植“春蕊牌”绿茶，由历年来市场销售行情知道，从每年的3月25日起的180天内，绿茶市场销售单位y(元)与上市时间t(天)的关系可以近似地用图①中的一条折线表示．绿茶的种植除了与气候、种植技术有关外，其种植的成本单价z(元)与上市时间t(天)的关系可以近似地用图②的抛物线表示．

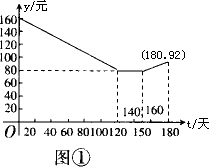
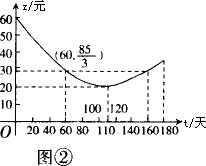
(1)直接写出图①中表示的市场销售单价y(元)与上市时间t(天)(t＞0)的函数关系式；

(2)求出图②中表示的种植成本单价z(元)与上市时间t(天)(t＞0)的函数关系式；

(3)认定市场销售单价减去种植成本为纯收益单价，问何时上市的绿茶收益单价最大？

(说明：市场销售单价和种植单价的单位：元/500克)

如图①，单杠高为2.2 m，两柱之间的距离为1.6 m，将一根绳子的两端系在立柱与铁杆AB结合处，绳子自然下垂呈近似抛物线形状．

(1)一身高0.7 m的小孩站在离立柱0.4 m处，其头部刚好接触在绳子上，求绳子的最低点C到地面的距离；

(2)为供孩子们荡秋千，把绳子剪断后，中间系一块长0.4 m的木板，除掉系木板用去的绳子后，两边的绳长正好各为2 m，木板与地面平行(如图②)，求这时木板到地面的距离．

(参考数据：≈1.8，≈1.9，≈2.1，精确到0.1 m．)

在直角坐标系中，有以A(－1，－1)，B(1，－1)，C(1，1)，D(－1，1)为顶点的方形．设正方形在直线y＝x上方及直线y＝－x＋2a上方的部分的面积为S．

(1)求当a＝0.5时，S的值；

(2)当a在实数范围内变化时，求S关于a的函数关系式．

心理学家研究发现，一般情况下，学生的注意力随着教师讲课的时间的变化而变化．讲课开始时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力随时间的变化规律如下：

y＝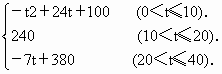

(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？

(2)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(3)一道数学难题，需要讲解24分钟，为了达到较好的效果，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲完这道题目？