某商场销售某种品牌的纯牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40元至70元之间．市场调查发现：若每箱以50元销售，平均每天可销售90箱，价格每降低1元，平均每天多销售3箱，价格每升高1元，平均每天少销售3箱．

(1)写出平均每天销售量y(箱)与每箱售价x(元)之间的函数关系式；(注明范围)

(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式；(每箱的利润＝售价－进价)

(3)求出(2)中二次函数图象的顶点坐标，并求当x＝40，70时，W的值，如图所示，在给出的坐标系中作出函数图象的草图；

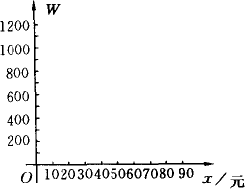
(4)根据函数图象，当牛奶售价为多少元时，平均每天的利润最大？最大利润为多少？

A，B两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查，提供了两个方面的信息，如下图所示，A调查表明：每个甲鱼池平均年产量由第1年的1万只甲鱼上升到第6年的2万只；B调查表明：甲鱼池个数由第1年的30个减少到第6年的10个．

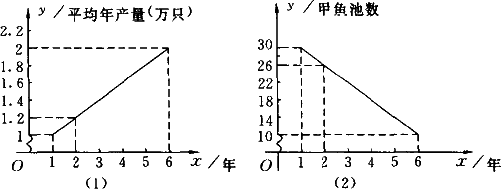
请你根据提供的信息回答下列问题．

(1)求第2年甲鱼池的个数及全县出产甲鱼的总数；

(2)到第6年这个县的甲鱼养殖业的规模比第1年扩大了还是缩小了？说明理由；

(3)哪一年的规模最大？说明理由．

已知关于x的二次函数y＝x²＋(k²－3k－4)x＋2k的图象与x轴从左至右交于A，B两点，且这两点关于原点对称．

(1)求k的值；

(2)在(1)的条件下，若反比例函数y＝的图象与二次函数y＝x²－(k²－3k－4)x＋2k的图象从左至右交于Q，R，S三点，且点Q的坐标为(－1，1)，如下图所示，求四边形AQBS的面积；

(3)在(1)，(2)的条件下，在x轴下方是否存在二次函数y＝x²＋(k²－3k－4)x＋2k的图象上的点P，使S_△PAB＝2S_△RAB？若存在，求出P点的坐标；若不存在，请说明理由．

如下图所示，在直角梯形ABCD中，AB∥CD，∠A＝90°，点E为AD的中点，P在腰BC上且不与B，C重合，连接PD，PE，AB＝18，CD＝6，AD＝16，设PC＝x，S_△PDE＝y．

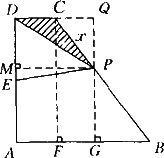
(1)求y与x之间的函数关系式；

(2)x为何值时，tan∠DPE＝？

(3)是否存在x，使S_△DPC＝S_梯形ABCD？

启明公司生产某种产品，每件产品的成本是3元，售价是4元，年销售量为10万件．为了获得更好的收益，公司准备拿出一定的资金做广告．根据经验，每年投入的广告费是x(万元)时，产品的年销售量将是原销售量的y倍，且y＝－＋x＋．如果把利润看作是销售总额减去成本费和广告费：

(1)试写出年利润S(万元)与广告费x(万元)的函数关系式，并计算广告费是多少万元时，公司获得的年利润最大，最大年利润是多少万元？

(2)把(1)中的最大利润留出3万元做广告，其余的资金投资新项目，现有6个项目可供选择，各项目每股投资金额和预计年收益如下表：

如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，则有几种符合要求的投资方式？写出每种投资方式所选的项目．

某跳水运动员进行10 m台跳水的训练时(将运动员看成一点)，在空中的运动路线如下图所示，为坐标系中经过原点O的一条抛物线(图中标出的数据为已知条件)，在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面10m，入水处距池边的距离为4 m，同时，运动员在距水面高度小于5 m以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误．

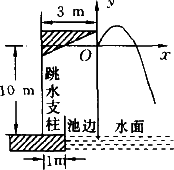
(1)求这条抛物线的解析式；

(2)在某次试跳时，测得运动员在空中的运动路线是(1)中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为3m，则此次跳水会不会失误？通过计算说明理由．

如下图所示，抛物线y＝－(x－m)²的顶点为A，直线l：y＝x－m与y轴的交点为B，其中m＞0．

(1)写出抛物线对称轴及顶点A的坐标(用含m的代数式表示)；

(2)证明点A在直线l上，并求∠OAB的度数；

(3)动点Q在抛物线对称轴上，抛物线上是否存在点P，使以P，Q，A为顶点的三角形与△OAB全等？若存在，求出m的值，并写出所有符合上述条件的P点坐标；若不存在，说明理由．

阅读并解答下列问题．

在给定的锐角△ABC中，求作一个正方形DEFG，使D，E落在BC边上，F，G分别落在AC，AB边上，作法如下．

第一步：画一个有三个顶点落在△ABC两边上的正方形；

第二步：连结并延长交AC于点F；

第三步：过F点作FE⊥BC，垂足为点E；

第四步：过F点作FG∥BC交AB于点G；

第五步：过G点作GD⊥BC，垂足为点D．

四边形DEFG为所求作的正方形．如图所示．

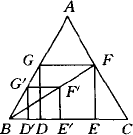
(1)证明上述所求作的四边形是正方形(EF＝FG)

(2)在△ABC中，如果BC＝6＋，∠ABC＝45°，∠BAC＝75°，求上述正方形DEFG的边长．

如图所示，在矩形ABCD中，M是BC上一动点，DE⊥AM，E为垂足，3AB＝2BC，并且AB，BC的长是方程x²－(k－2)x＋2k＝0的两个根．

(1)求k的值；

(2)当△AED的面积是△DEM的3倍时，求BM的长．

已知直线l垂直于x轴，垂足为D(2，0)，一次函数y＝kx＋b的图象与x轴交于点B，与y轴交于点C，与直线l交于点A．

(1)当B，C两点的坐标分别为B(3，0)，C(0，－6)时，若直线m与直线BC关于直线l对称，求直线m的关系式；

(2)求满足条件(1)以A为顶点，且过点B的抛物线的关系式；

(3)在一次函数y＝kx＋b(k＞0)中，是否存在实数k，b，使△BOC和△BDA同时为等腰直角三角形？若存在，请证明；若不存在，说明理由．