在平面直角坐标系中，A(－1，0)，B(3，0)．

(1)若抛物线过A，B两点，且与y轴交于点(0，－3)，求此抛物线的顶点坐标：

(2)如图(1)，小敏发现所有过A，B两点的抛物线，如果与y轴负半轴交于点C，M为抛物线的顶点，那么△ACM与△ACB的面积比不变，请你求出这个比值：

(3)若对称轴是AB的中垂线l的抛物线与x轴交于点E，F，与y轴交于点C，过C作CP∥x轴交l于点P，M为此抛物线的顶点．若四边形PEMF是有一个内角为60°的菱形，求此抛物线的解析式．

已知：抛物线y＝－x²－(m＋3)x＋m²－12与x轴交于A(x₁，0)、B(x₂，0)两点，且x₁＜0，x₂＞0，抛物线与y轴交于点C，OB＝2OA．

(1)求抛物线的解析式；

(2)在x轴上，点A的左侧，求一点E，使△ECO与△CAO相似，并说明直线EC经过(1)中抛物线的顶点D；

(3)过(2)中的点E的直线y＝x＋b与(1)中的抛物线相交于M、N两点，分别过M、N作x轴的垂线，垂足为、，点P为线段MN上一点，点P的横坐标为t，过点P作平行于y轴的直线交(1)中的所求抛物线于点Q．是否存在t值，使∶S_△QMN＝35∶12，若存在，求出满足条件的t值；若不存在，请说明理由．

已知二次函数y＝ax²＋bx＋c，当x＝1时，y有最大值＝4，且|a|＝1，(1)求它的解析式；(2)若上述图象与x轴交点为A、B，直线y＝kx＋m(k＜0)过A、B中的一点及函数图象顶点G，且与y轴交于C点，求直线解析式；(3)求原点到所求直线的距离

已知：二次函数y＝x²－kx＋k＋4的图象与y轴交于点C，且与x轴的正半轴交于A，B两点(点A在点B左侧)，若A，B两点的横坐标为整数，

(1)确定这个二次函数的解析式并求它的顶点坐标；

(2)若点D的坐标是(0，6)，点P(t，0)是线段AB上的一个动点，它可与点A重合，但不与点B重合．设四边形PBCD的面积为S，求S与t的函数关系式；

(3)若点P与点A重合，得到四边形ABCD，以四边形ABCD的一边为边，画一个三角形，使它的面积等于四边形ABCD的面积，并注明三角形高线的长．再利用“等底等高的三角形面积相等”的知识，画一个三角形，使它的面积等于四边形ABCD的面积(画示意图，不写计算和证明过程)．

阅读下面的解题过程，然后解答后面的问题．

　　题目：如图(1)，已知正方形ABCD中，点M是AB的中点，点E是AB延长线上的一点，MN⊥DM交∠CBE的平分线BN于点N．试说明MD＝MN．

　　解：在AD上取一点F，使AF＝AM，连结MF．

　　因为ABCD是正方形，

　　所以DF＝MB，∠1＋∠AMD＝90°．

　　因为DM⊥MN，

　　所以∠AMD＋∠2＝90°．

　　所以∠1＝∠2．

　　因为BN平分∠CBE，

　　所以∠MBN＝135°＝∠DFM．

　　所以△DFM≌△MBN．

　　所以DM＝MN．

(1)在上述说理过程中，“点M是AB的中点”这个条件没有用到，若将这个条件改为“点M是AB上的任意一点”，或“点M是AB延长线上的任意一点”，或“点M是BA延长线上的任意一点”，则结论“DM＝MN”还成立吗？请说明理由；

(2)如图(2)，在正三角形ABC中，若AE＝CD，则∠BFE＝60°；如图(3)，在正方形ABCD中，若DE＝CF，则∠AGF＝90°．这里的两个结论“∠BFE＝60°”和“∠AGF＝90，分别与题目的背景条件“正三角形ABC”和“正方形ABCD”有关．你能否改编一道题目，改变上述题目的背景“正方形ABCD”，并相应改变条件“MN⊥DM”，而其余条件与结论不变？请说明所编题目的正确性．

“三等分角”是数学史上一个著名问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如下图)．将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数y＝的图像交于点P，以P为圆心、以2OP为半径作弧交图像于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连结OM得到∠MOB，则∠MOB＝∠AOB．

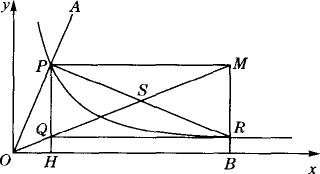
要明白帕普斯的方法，请研究以下问题：

(1)设P、R，求直线OM对应的函数表达式(用含a，b的代数式表示)；

(2)分别过点P和R作y轴和x轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB＝∠AOB；

(3)应用上述方法得到的结论，你如何三等分一个钝角(用文字简要说明)．

如图，形如量角器的半圆O的直径DE＝12 cm，形如三角板的△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝12 cm．半圆O以2 cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t (s)，当t＝0 s时，半圆O在△ABC的左侧，OC＝8 cm．

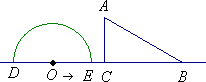
(1)当t为何值时，△ABC的一边所在的直线与半圆O所在的圆相切？

(2)当△ABC的一边所在的直线与半圆O所在的圆相切时，如果半圆O与直径E围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．

如图1，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8 cm，矩形ABCD的长和宽分别为8 cm和2 cm，C点和M点重合，BC和MN在一条直线上．令Rt△PMN不动，矩形ABCD沿MN所在直线向右以每秒1 cm的速度移动(如图2)，直到C点与N点重合为止．设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y cm²．求y与x之间的函数关系式．

如图，已知四边形ABCD内接于⊙O，A是弧BDC的中点．AE⊥AC于A，与⊙O及CB的延长线分别交于点F、E，且弧BF＝弧AD，EM切⊙O于M．

(1)求证：△ADC∽△EBA；

(2)求证：AC²＝BC·CE

(3)如果AB＝2，EM＝3，求tan∠CAD的值．

已知⊙O的半径为1，以O为原点，建立如图所示的直角坐标系．有一个正方形ABCD，顶点B的坐标为(－，0)，顶点A在x轴上方，顶点D在⊙O上运动．

(1)当点D运动到与点A、O在一条直线上时，CD与⊙O相切吗？如果相切，请说明理由，并求出OD所在直线对应的函数表达式；如果不相切，也请说明理由；

(2)设点D的横坐标为x，正方形ABCD的面积为S，求出S与x的函数关系式，并求出S的最大值和最小值．