如图，在海面上产生了一股强台风，台风中心(记为点M)位于滨海市(记作点A)的南偏西15°，距离为61千米，且位于临海市(记作点B)正西方向60千米处．台风中心正以72千米/时的速度沿北偏东60°(射线MN的方向)的方向移动(假设台风在移动过程中的风力保持不变)，距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭．

(1)滨海市、临海市是否会受到此次台风的侵袭？请说明理由．

(2)若受到此次台风侵袭，该城市受到台风侵袭的持续时间有多少小时？

某地有一种可食用的野生菌，上市时，外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将会每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这类野生菌在冷库中最多保存160天，同时，平均每天有3千克的野生菌损坏不能出售．

(1)设x天后每千克该野生菌的市场价格为y元，试写出y与x之间的函数关系式．

(2)若存放x天后，将这批野生菌一次性出售，设这批野生菌的销售总额为P元，试写出P与x之间的函数关系式．

(3)李经理将这批野生菌存放多少天后出售可获得最大利润W元？

(利润＝销售总额－收购成本－各种费用)

在平面直角坐标系中给定以下五个点A(－3，0)，B(－1，4)，C(0，3)，D(，)，E(1，0)．

(1)请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的表达式；

(2)求该抛物线的顶点坐标和对称轴，并画出草图；

(3)已知点F(－1，)在抛物线的对称轴上，直线y＝过点G(－1，)且垂直于对称轴．验证：以点E(1，0)为圆心，EF为半径的圆与直线y＝相切．请你进一步验证，以抛物线上的点D(，)为圆心，DF为半径的圆也与直线y＝相切．由此你能猜想到怎样的结论2．

已知二次函数y＝x²＋bx＋c的图象经过A(c，－2)，．

求证：这个二次函数的对称轴是x＝3．

题目中的矩形阴影部分是一段被墨水污染无法辨认的文字．

(1)根据题目中的现有信息，你能否求出二次函数表达式？若能，请写出解答过程，并画出二次函数图象；若不能，请说明理由．

(2)请你根据已有的信息，在原题的矩形阴影中，填上一个适当的条件，把原题补充完整．

如图，在平面直角坐标系xOy中，经过点A、C、B的抛物线的一部分与经过点A、E、B的抛物线的一部分组合成一条封闭曲线，我们把这条封闭曲线称为“双抛物线”．已知P为AB的中点，且P(－1，0)，C(－1，1)，E(0，－3)，S_△CPA＝1．

(1)试求“双抛物线”中经过点A、E、B的抛物线的解析式；

(2)若点F在“双抛物线”上，且S_△FAP＝S_△CAP，请你直接写出点F的坐标；

(3)如果一条直线与“双抛物线”只有一个交点，那么这条直线叫做“双抛物线”的切线．若过点E与x轴平行的直线与“双抛物线”交于点G，求经过点G的“双抛物线”的切线的解析式．

如图，⊙O的弦AD∥BC，过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及其延长线分别交AC、BC于点G、F．

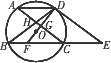
(1)求证：DF垂直平分AC；

(2)求证：FC＝CE；

(3)若弦AD＝5 cm，AC＝8 cm，求⊙O的半径．

下图①是边长分别为4和3的两个等边三角形纸片ABC和叠放在一起(C与重合)．

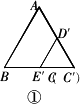
(1)操作：固定△ABC，将△绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于点F(如图②)．

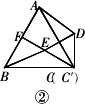
探究：在图②中，线段BE与AD之间有怎样的大小关系？试证明你的结论．

(2)操作：将图②中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，CF为∠ACB的平分线，平移后的△CDE设为△PQR(如图③)．

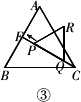
探究：设△PQR移动的时间为xs，△PQR与△AFC重叠部分的面积为y，求y与x之间的函数关系式，并写出函数自变量x的取值范围．

(3)操作：将图①中△固定，将△ABC移动，使顶点C落在的中点，边BC交于点M，边AC交于点N，设∠AC＝α(30°＜α＜90°)(如图④)．

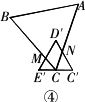
探究：在图④中，线段N·M的值是否随α的变化而变化？如果没有变化，请求出N·M的值；如果有变化，请说明理由．

杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体(看成一点)的路线是抛物线y＝－x²＋3x＋1的一部分，如图．

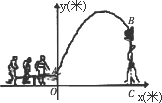
(1)求演员弹跳离地面的最大高度；

(2)已知人梯高BC＝3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．

已知二次函数y＝x²＋bx＋c与x轴交于A(－1，0)、B(1，0)两点．

(1)求这个二次函数的关系式；

(2)若有一半径为r的⊙P，且圆心P在抛物线上运动，当⊙P与两坐标轴都相切时，求半径r的值；

(3)半径为1的⊙P在抛物线上，当点P的纵坐标在什么范围内取值时，⊙P与y轴相离、相交？

如图，已知⊙O的半径OA＝6，AP是半圆的切线，点C是半圆上的一动点(不与点A、B重合)，过点C作CD⊥AP于点D，记∠COA＝α．

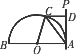
(1)当α＝60°时，求CD的长；

(2)α为何值时，CD与⊙O相切？说明理由．