
科目: 来源:1+1轻巧夺冠优化训练九年级数学上 北京课改版 题型:047
已知:AB是圆O的直径,C是圆O上一点,连接AC,过C作CD⊥AB于D,E是AB上一点,直线CE与圆O交于点F,连接AF与CD延长线交于G.
求证:AC2=AG·AF.

查看答案和解析>>
科目: 来源:1+1轻巧夺冠优化训练九年级数学上 北京课改版 题型:047
如图所示,已知P、C是以AB为直径的半圆O上的两点,AB=10,弧PC的长为![]() ,连接PB交AC于M.
,连接PB交AC于M.
求证:MC=BC.

查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:047
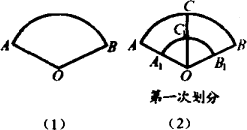
下图中,图(1)是一个扇形AOB,将其作如下划分:
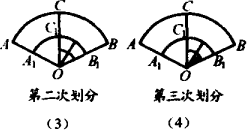
第一次划分:如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线,得到扇形的总数为6个,分别为:扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;
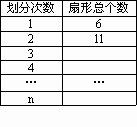
第二次划分:如图(3)所示,在扇形C1OB1中,按上述划分方式继续划分,可以得到扇形的总数为11个;
第三次划分:如图(4)所示;
……
依次划分下去.
(1)根据题意,完成下表:
(2)根据上表,请你判断按上述划分方式,能否得到扇形的总数为2005个?为什么?
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:047
如图所示,AO是△ABC的中线,⊙O与AB边相切于点D.

(1)要使⊙O与AC边也相切,应增加条件________.(任写一个)
(2)增加条件后,请你证明⊙O与AC边相切.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:047
抛物线与x轴相交于A(-1,0),B(4,0),与y轴相交于C(0,2).
(1)求抛物线的解析式;
(2)是否存在经过点M(-2,0)的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:047
如图,抛物线y=![]() x2-x+
x2-x+![]() 的顶点为M,过点M分别引x轴、y轴的垂线,垂足分别为A,B,将矩形OAMB绕原点O逆时针旋转90°得到矩形
的顶点为M,过点M分别引x轴、y轴的垂线,垂足分别为A,B,将矩形OAMB绕原点O逆时针旋转90°得到矩形![]() .
.
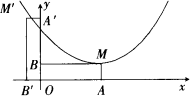
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 能否在此抛物线上?若能,请说明理由;若不能,矩形
能否在此抛物线上?若能,请说明理由;若不能,矩形![]() 应向右或向左平移多少个单位,才能使点
应向右或向左平移多少个单位,才能使点![]() 恰好在此抛物线上?
恰好在此抛物线上?
查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:047
| |||||||||||||||
查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:047
如图所示,设P为正△ABC外接圆⊙O劣弧![]() 上任一点,弦AP与弦BC交于D,连结BP,CP.求证:PB,PC是方程x2-PA·x+PA·PD=0的两个根.
上任一点,弦AP与弦BC交于D,连结BP,CP.求证:PB,PC是方程x2-PA·x+PA·PD=0的两个根.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com