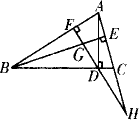
如图所示，已知△ABC中，AD⊥BC于D，BE⊥AC于E，DF⊥AB于F，交BE于G，FD、AC的延长线交于H，求证：DF²＝FG·FH．

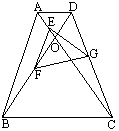
如图，等腰梯形ABCD中，AD∥BC，E、F、G分别为AO、BO、CD的中点，∠BOC＝．求证：△EFG为等边三角形．

如图，等腰梯形ABCD中，AD∥BC，对角线AC、BD相互垂直，且AD＝m，BC＝n.求证：(m＋n)²＝4S_梯形ABCD

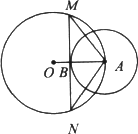
已知A为⊙O上一点，B为⊙A与OA的交点，⊙A与⊙O的半径分别为r、R，且r＜R．如图，过点B作⊙A的切线与⊙O交于M、N两点．求证：AM·AN＝2Rr．

如图，已知：⊙O₁与⊙O₂相交于点A、B，过点B作CD⊥AB，分别交⊙O₁和⊙O₂于点C、D．

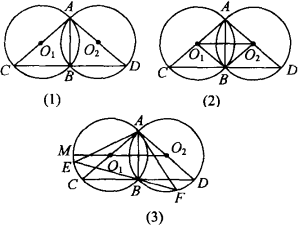
(1)如图(1)，求证：AC是⊙O₁的直径．

(2)若AC＝AD．

①如图(2)，连结BO₂、O₁O₂，求证：四边形O₁CBO₂是平行四边形；

②若点O₂在⊙O₁外，延长O₂O₁交⊙O₁于点M，在劣弧上任取一点E(点E与点B不重合)．EB的延长线交优弧于点F，如图(3)所示．连结AE、AF．则AE________AB(请在横线上填上“≥”“≤”“＜”“＞”这四个不等号中的一个)，并加以证明．

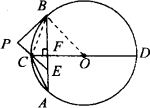
如图，已知点A在⊙O上，PC交⊙O于B、C两点．

(1)若PA是⊙O的切线，求证：PA²＝PB·PC；

(2)若PA²＝PB·PC，求证：PA是⊙O的切线．

如图，PC切⊙O于点C，过圆心的割线PAB交⊙O于A、B两点，BE⊥PE，垂足为E，BE交⊙O于点D，F是PC上一点，且PF＝AF，FA的延长线交⊙O于点G．

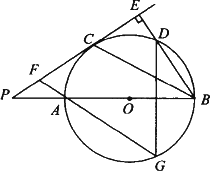
求证：(1)∠FGD＝2∠PBC；

(2)．

如图，△ABC内接于⊙O，AD平分∠BAC，交直线BC于点E，交⊙O于点D．

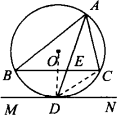
(1)过点D作MN∥BC，求证：MN是⊙O的切线；

(2)求证：AB·AC＝AD·AE；

(3)如图，AE平分∠BAC的外角∠FAC，交BC的延长线于点E，EA的延长线交⊙O于点D．结论AB·AC＝AD·AE是否仍然成立？如果成立，请写出证明过程；如果不成立，请说明理由．

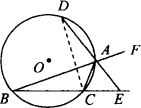
如图，已知⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA＝EC．

(1)求证：AC²＝AE·AB；

(2)延长EC到点P，连结PB，若PB＝PE，试判断PB与⊙O的位置关系，并说明理由．

请看下列例题及解答：

[例]如图，四边形ABCD中，AB∥CD，AD＝DC＝DB＝6.5，BC＝5，求对角线AC的长．

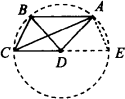
解答：以D为圆心，AD的长为半径作⊙D．显然⊙D经过点A、B、C．延长CD交⊙D于点E，连结AE，根据本节《探究体验》可知四边形ABCE为等腰梯形，故AE＝BC＝5．

∵CE为⊙D直径，∴∠CAE＝90°．

在Rt△ACE中，CE＝2AD＝13，AE＝5．

∴AC＝＝12．

请构造辅助圆解决下列问题：如图，在四边形ABCD中，AB＝AC＝AD，且∠DBC＝2∠BDC．求证：∠DAB＝3∠BAC．