
科目: 来源:鼎尖助学系列—同步练习(数学 八年级下册)、数据的整理与初步处理 扇形统计图(2) 题型:059
如图是某报在2003年3月23日美国对伊拉克战争开战第三天刊登的一个关于美国石油来源地区分布的扇形统计图,你能从中获得哪些信息?美国为什么要侵略一个主权国家?

查看答案和解析>>
科目: 来源:鼎尖助学系列—同步练习(数学 八年级下册)、数据的整理与初步处理 扇形统计图(2) 题型:059
| |||||||||||
查看答案和解析>>
科目: 来源:鼎尖助学系列—同步练习(数学 八年级下册)、数据的整理与初步处理 扇形统计图(2) 题型:059
我国政府在农村扶贫工作中取得了显著成效,据国家统计局公布的数据表明,2004年末我国农村绝对贫困人口为2610万人(比上年末减少290万人),其中东部地区为374万人,中部地区为932万人,西部地区为1305万人,请用扇形统计图表示出2004年末这三个地区农村绝对贫困人口分布的比例(要在图中注明各部分所占的比例).

查看答案和解析>>
科目: 来源:漫游数学世界八年级(上) 题型:059
小明始终认为抛掷两枚硬币出现“一正一反”和出现“两个正面”的概率一样.小华想用实验的方法说服他,但手头又没有硬币.你能帮他想想办法吗?
查看答案和解析>>
科目: 来源:漫游数学世界八年级(上) 题型:059
小王和小张每人抛掷两颗普通的正六面体骰子,并将骰子落地后出现点数之和大于6的频率描述如下:
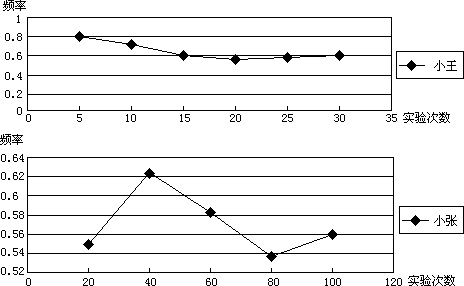
根据折线图,小王估计骰子落地后出现点数之和大于6的概率约为60%,小张估计骰子落地后出现点数之和大于6的概率约为56%.你的看法怎样?
查看答案和解析>>
科目: 来源:漫游数学世界八年级(上) 题型:059
甲乙轮流抛掷一个质量分布均匀的硬币.甲已经抛了5次,一次也没出现正面;乙也抛了5次,有3次出现了正面.下一次抛掷时谁得到正面的机会比较大?
查看答案和解析>>
科目: 来源:四川省眉山市仁寿联校2012届九年级上学期期中检测数学试题 题型:059
(1)如图:靠着22 m的房屋后墙,围一块150 m2的矩形鸡场,现在有篱笆共40 m.求矩形的长、宽各多少米?

(2)若把“围一块150 m2的矩形鸡场”改为“围一块S m2的矩形鸡场”其它条件不变,能否使S最大.若能,请你求出此时矩形的长、宽及最大面积;若不能,请你说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 华师大八年级版 2009-2010学年 第18期 总第174期 华师大版 题型:059
已知正方形ABCD的边长为4,点E是边CD上一个动点,以CE为一条直角边作等腰直角三角形CEF,连结BF、FD、BD,则BD与CF的位置关系是________.
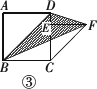
(1)如图①,当CE=4(即点E与点D重合)时,△BDF的面积为________;
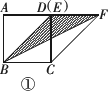
(2)如图②,当CE=2(即点E为CD的中点)时,△BDF的面积为________;
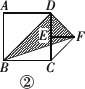
(3)如图③,当CE=3时,△BDF的面积为________;
(4)如图④,根据上述计算的结果,当点E为CD边上任意一点时,请提出你对△BDF的面积与正方形ABCD的面积之间的关系的猜想,并证明你的猜想;

(5)如图⑤,当点E为CD的延长线上任意一点时,请判断(4)中的结论是否仍然成立.(不要求说明理由)
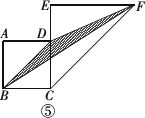
查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
在研究“三角形的三个内角和等于180°”的证明方法时,小明和小虎分别给出了下列证法:
小明:在△ABC中,延长BC到点D(如图),
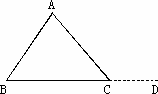
所以∠ACD=∠A+∠B.(三角形的一个外角等于与它不相邻的两个内角的和)
又因为∠ACD+∠ACB=180°,(平角定义)
所以∠A+∠B+∠ACB=180°.(等量代换)
小虎:在△ABC中,过点A作AD⊥BC(如图),

所以∠ADC=∠ADB=90°.(直角定义)
所以∠DAC+∠C=90°,∠B+∠BAD=90°.(直角三角形的两锐角互余)
所以∠DAC+∠C+∠B+∠BAD=180°,
即∠BAC+∠B+∠C=180°.
请你对上述两名同学的证法给出评价,并写出一种你认为较简单的证明三角形内角和定理的方法.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第17期 总第173期 北师大版 题型:059
在平面直角坐标系中,给出以下五点A(-2,0),B(1,0),C(4,0),D(-2,![]() ),E(0,-6),从这五点中选取三点,使经过这三点的抛物线满足以平行于y轴的直线为对称轴.我们约定:把经过三点A、E、B的抛物线表示为抛物线AEB(如图所示).
),E(0,-6),从这五点中选取三点,使经过这三点的抛物线满足以平行于y轴的直线为对称轴.我们约定:把经过三点A、E、B的抛物线表示为抛物线AEB(如图所示).
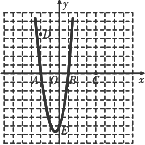
(1)问符合条件的抛物线还有哪几条?不求解析式请用约定的方法表示出来;
(2)在(1)中是否存在这样的一条抛物线,它与余下的两点所确定的直线不相交?如果存在,试求抛物线及直线的解析式;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com