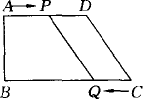
如图所示，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24 cm，AB＝8 cm，BC＝26 cm，动点P从A开始沿AD边向D以1 cm/s的速度运动，动点Q从点C开始沿CB边向B以3 cm/s的速度运动，P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒，t分别为何值时，四边形PQCD为平行四边形？等腰梯形？

已知四边形ABCD中，AB＝DC，AC＝BD，试讨论ABCD可能是什么形状的四边形，并证明你的结论．

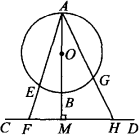
如图，已知AB是⊙O的直径，AB垂直于弦CD，垂足为M，弦AE与CD交于F，则有结论AD²＝AE·AF成立(不要求证明)．

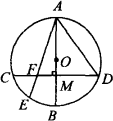
(1)若将弦CD向下平移至与⊙O相切于B点时，如图，则AE·AF是否等于AG²？如果不相等，请探求AE·AF，等于哪两条线段的积？并给出证明．

(2)当CD继续向下平移至与⊙O相离时，如图，在(1)中探求的结论是否还成立，并说明理由．

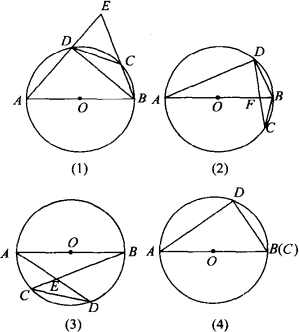
已知：如图(1)，在⊙O中，弦AB＝2，CD＝1，AD⊥BD．直线AD、BC相交于点E．(1)求∠E的度数；(2)如果点C，D在⊙O上运动，且保持弦CD的长度不变．那么，直线AD，BC相交所成锐角的大小是否改变？试就以下三种情况进行探究，并说明理由(图形未画完整，请你根据需要补全)．①如图(2)，弦AB与弦CD交于点F；②如图(3)，弦AB与弦CD不相交；③如图(4)，点B与点C重合．

如图，⊙O₁与⊙O₂内切于点P，⊙O₁的半径为r，⊙O₂的半径为R，R＝3r，点B为⊙O₂上的一点，(不与P重合)，PB交⊙O₁于点A．

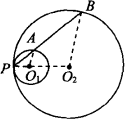
(1)求PA∶AB的值；

(2)当点B在⊙O₂上运动时，PA∶AB的值是否会发生改变？(直接回答，不必说明理由)．

　　如图，已知：如图(1)，AB是⊙O的直径，P是AB上的一点(与A、B不重合)．QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：

　　证明：连结OC．

　　∵OA＝OC，∴∠A＝∠1．

　　∵CD切⊙O于C点，

　　∴∠OCD＝90°，

　　∴∠1＋∠2＝90°，

　　∴∠A＋∠2＝90°．

　　在Rt△QPA中，∠QPA＝90°，

　　∴∠A＋∠Q＝90°，

　　∴∠2＝∠Q．∴DQ＝DC．

　　即△CDQ是等腰三角形．

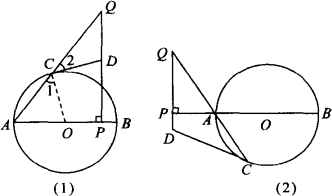
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图(2)所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

如图，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直AB于点F，交BC于点G，连结PC，∠BAC＝∠BCP，求解下列问题：

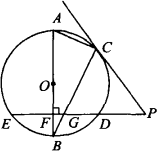
(1)求证：CP是⊙O的切线；

(2)当∠ABC＝30°，BG＝，CG＝时，求以PD、PE的长为两根的一元二次方程；

(3)若(1)的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可使结论BG²＝BF·BO成立？试写出你的猜想，并说明理由．