
科目: 来源:学习周报 数学 华师大八年级版 2009-2010学年 第19~26期 总第175~182期 华师大版 题型:059
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论S△PBC=S△PAC+S△PCD成立.
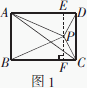
理由:过点P作EF⊥BC,分别交AD、BC于E、F两点.
因为S△PBC+S△PAD=
所以S△PBC=S△PAC+S△PCD.
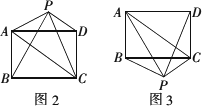
请你参考上述信息,当点P分别在图2、图3中的位置时,又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第19期 总第175期 沪科版 题型:059
如图
1,线段PB过圆心O,交⊙O于A、B两点,PC切⊙O于点C,过点A作AD⊥PC,垂足为D,连接AC、BC.
(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线PC变为图2中的割线PE,且PE与⊙O交于C、E两点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);
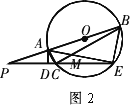
(3)在图2中,证明:AD·AB=AC·AE.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第6期 总第162期 沪科版 题型:059
如图,矩形
ABCD中,AB=8厘米,BC=12厘米,P、Q分别是AB、BC上运动的两点.若点P自点A出发,以1厘米/秒的速度沿AB方向运动,同时点Q自点B出发以2厘米/秒的速度沿BC方向运动.设点P运动的时间为t秒,当t为何值时,以P、B、Q为顶点的三角形与△BCD相似?
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第6期 总第162期 沪科版 题型:059
如图,△
ABC中,∠B=∠C=α(0°<α<60°).将一个三角尺中30°角的顶点P放在BC边上,当点P在BC边上移动时,三角尺中30°角的一条边始终过点A,另一条边交AC边于点Q,P、Q不与三角形的顶点重合.设∠CPQ=β,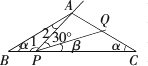
(1)用α、β表示∠1和∠2;
(2)①当β在许可范围内变化,α取何值时,总有△ABP∽△PCQ?
②当α在许可范围内变化,β取何值时,总有△ABP∽△QCP?
(3)有无可能使△ABP、△QPC、△ABC两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
如图,△ABC中,AB=AC=10 cm,BC=8 cm,D为AB的中点.如果点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
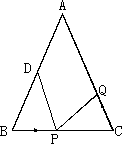
(1)若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够出现△BPD与△CQP全等?
查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
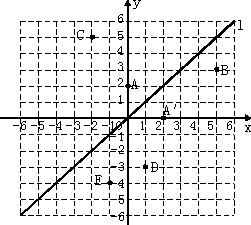
实验与探究:
(1)由图观察易知点A(0,2)关于直线l的对称点![]() 的坐标为(2,0),请在图中分别标出点B(5,3)、C(-2,5)关于直线l的对称点
的坐标为(2,0),请在图中分别标出点B(5,3)、C(-2,5)关于直线l的对称点![]() 、
、![]() 的位置,并写出这两个点的坐标:
的位置,并写出这两个点的坐标:![]() ________、
________、![]() ________;
________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于第一、三象限的角平分线l的对称点![]() 的坐标为________(不必证明);
的坐标为________(不必证明);
运用与拓广:
(3)已知点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出点Q的坐标.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线.
(1)如图,若点B、C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.求证:BD=DE+CE;
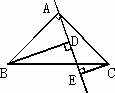
(2)若直线AE绕点A旋转到下图的位置时(BD<CE),其余条件不变,问BD与DE、CE的关于如何?并证明你的结论.

查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
如图,已知C为线段AB上一点,△ACM和△BCN都是等边三角形.

(1)求证:AN=BM;
(2)若把原题中“△ACM和△BCN都是等边三角形”换成“四边形ACMF和四边形CBEN都是正方形”(如图所示),那么AN与BM的关系如何?请说明理由.

查看答案和解析>>
科目: 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:059
如图,在等边三角形ABC中,AE=CD,BD与CE相交于点F.
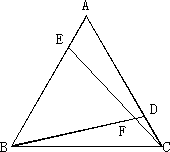
(1)求证:△ABD≌△BCE;
(2)求出∠BFE的度数;
(3)根据已知条件能直接判断△ACE与△CBD全等吗?如果全等,请说出全等的条件,不必写出过程;如果不能,说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第21期 总第177期 北师大版 题型:059
已知∠MAN=30°,O为边AN上的一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,设AD=x.
(1)如图,当x取何值时,⊙O与AM相切.
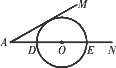
(2)如图,当x取何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
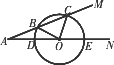
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com