
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:059
如图(1)所示,矩形ABCD的两条边在坐标轴上,点D与原点重合,对角线BD所在直线的函数关系式为y=![]() x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.


(1)求矩形ABCD的周长.
(2)如图(2)所示,图形运动到第5秒时,求点P的坐标.
(3)设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式.
(4)当点P在线段AB或BC上运动时,过点P作x轴、y轴的垂线,垂足分别为E、F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:059
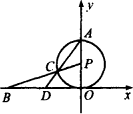
已知:如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(-2![]() ,0)在x轴上.连结BP交⊙P于点C,连结AC并延长交x轴于点D.
,0)在x轴上.连结BP交⊙P于点C,连结AC并延长交x轴于点D.
(1)求线段BC的长;
(2)求直线AC的关系式;
(3)当点B在x轴上移动时,是否存在点B,使△BOP相似于△AOD?若存在,求出符合条件的点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:059
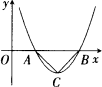
如下图所示,二次函数图象的顶点坐标为C(2,-1),二次函数的图象在x轴上截得的线段AB的长为2.
(1)求证:△ACB是等腰直角三角形;
(2)求二次函数的解析式;
(3)在抛物线上是否存在点P,使△PAC是等腰三角形,若存在,请求出点P的坐标,不能求出时,请给出横纵坐标的范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:059
抛物线y=x2-2x-3与x轴交于A,B两点(A点在B点的左侧).
(1)抛物线上有一个动点P,求当点P在抛物线上滑动到什么位置时,△PAB的面积为10,并求出此时点P的坐标;
(2)抛物线交y轴于点C.在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:059
某学校研究性学习小组在研究二次函数及其图象的问题时,发现了两个重要结论:
①抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;
②抛物线y=ax2+2x+3的顶点横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到点A;顶点横坐标增加
得到点A;顶点横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() 得到点B,则A,B两点仍然在抛物线y=ax2+2x+3上.
得到点B,则A,B两点仍然在抛物线y=ax2+2x+3上.
(1)探索当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是抛物线的顶点,请你找出来,并说明理由;
(3)请你参考第二个发现写出关于抛物线y=ax2+bx+c顶点的结论,并说明理由.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:059
如图,过y轴上点A(0,1)作AC平行于x轴,交抛物线y=x2(x≥0)于点B,交抛物线y=0.25x2(x≥0)于点C;过点C作CD平行于y轴,交抛物线y=x2于点D;过点D作DE平行于x轴,交抛物线y=0.25x2于点E.
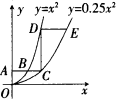
(1)求AB∶BC的值;
(2)判断O,B,E三点是否在同一直线上,如果在,写出直线的解析式;如果不在,请说明理由.
查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:059
| |||||||||||||||
查看答案和解析>>
科目: 来源:中学学习一本通 数学八年级下册 北师大新课标 题型:059
| |||||||||||
查看答案和解析>>
科目: 来源:福建省连江四中教研片2011-2012学年八年级上学期期中联考数学试题 题型:059
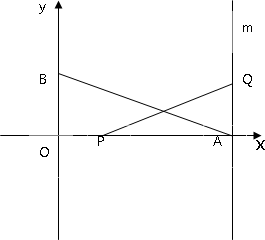
如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标是(0,5).直线m过点A且垂直于x轴.点p在线段OA上运动(含O、A)、点Q是直线m上的动点,且线段PQ=AB.问点P、Q在运动过程中是否存在使△ABO和△QPA全等情况?如果存在请求出典P、Q的坐标;不存在请说明理由.
查看答案和解析>>
科目: 来源:江苏省大丰市2010-2011学年八年级上学期期末学情调研数学试题 题型:059
(1)如图,在正方形ABCD中,点E,F分别在边BC、CD上,AE,BF交于点O,∠AOF=90°.
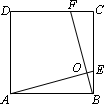
求证:AE=BF.
(2)如图,在正方形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°, EF=4.求GH的长.
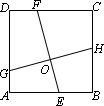
(3)如图,在矩形ABCD中,AB=3AD,点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4,求GH的长.
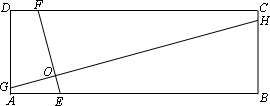
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com