
科目: 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:059
某校研究性学习小组在研究有关二次函数及其图象性质的问题时,发现了两个重要的结论:一是发现抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线y=ax2+2x+3的顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
(1)请你协助探求出当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用“一般——特殊——一般”的思想,你还能发现什么?你能用数学语言将你的猜想表达出来吗?你的猜想能成立吗?若能成立,请说明理由.
查看答案和解析>>
科目: 来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版 题型:059
已知抛物线y=![]() x2+bx+c的顶点坐标是(1,
x2+bx+c的顶点坐标是(1,![]() ).
).
(1)求抛物线的解析式;
(2)若直线y=kx(k>0)分别与抛物线交于两个不同的点A、B,与直线y=-x+4相交于点P,求![]() 的值;
的值;
(3)在(2)中,是否存在k的值,使A、B两点的纵坐标之和等于4?如果存在,求出k的值,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:新课程 新理念 新思维·训练编·数学 九年级下册(苏教版) 苏教版 题型:059
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为=-
),直线l2的函数表达式为=-![]() x+
x+![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
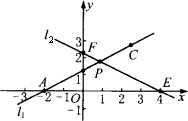
(1)填空:直线l1的函数表达式是________,交点P的坐标是________,∠FPB的度数是________;
(2)当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=![]() -2时a的值.
-2时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=![]() -2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
-2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:059
如下图所示,在矩形ABCD中,AB=20 cm,BC=4 cm,点P从A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从C开始沿CD边以1 cm/s的速度移动,如果点P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).

(1)t为何值时,四边形APQD为矩形?
(2)如下图所示,如果⊙P和⊙Q的半径都是2 cm,那么t为何值时,⊙P和⊙Q外切?
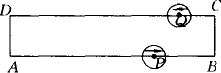
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
已知关于x的一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.

(1)求b,c的值(用含m的代数式表示);
(2)设抛物线y=-x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,如图所示,若点D的坐标为(0,-2),且AD2+BD2=25,求抛物线的关系式及点C的坐标;
(3)在(2)中所得的抛物线上是否存在点P,使得PC=PD?若存在,求出P点的坐标;若不存在,请说明理由;
(4)在(2)中所得的抛物线上是否存在点P,使得△PCD是等腰三角形?若存在,指出满足条件的P点的个数;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
阅读题.
(1)如图所示,设正方形ABCD的面积为S,它的两条对角线与一组对边所围成的两个三角形面积为S1,S2,则![]() 三者之间存在的等量关系为________;
三者之间存在的等量关系为________;
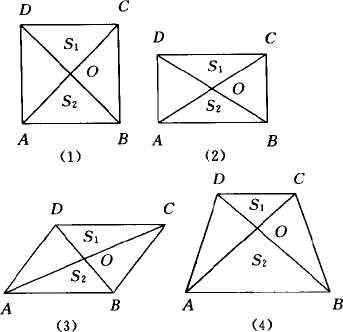
(2)将第(1)问中的正方形改为矩形后,其余条件不变,则第(1)问中的等量关系是否成立?
(3)将第(1)问中的正方形改为平行四边形后,依照第(1)问写一个命题并判断真假;(不要求证明)
(4)设梯形的面积为S,梯形的两条对角线与两底边所夹的三角形面积为S1,S2,则![]() 三者之间有何等量关系,并证明你的结论;
三者之间有何等量关系,并证明你的结论;
(5)根据(1)至(4)你可以归纳出的结论:________.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
如图(1)所示,梯形ABCD中,AD∥BC,AB=DC.

(1)如果P,E,F分别是BC,AC,BD的中点.求证AB=PE+PF;
(2)如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC.
如图(2)所示,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目: 来源:标准大考卷·初中数学AB卷 九年级(上册) (课标华东师大版) (第3版) 课标华东师大版 第3版 题型:059
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙![]() 交x轴于D点,过点D作DF⊥AE于点F.
交x轴于D点,过点D作DF⊥AE于点F.
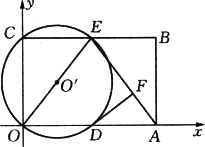
(1)求OA、OC的长;
解:
(2)求证:DF为⊙![]() 的切线;
的切线;
证明:
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙![]() 外”.你同意他的看法吗?请充分说明理由.
外”.你同意他的看法吗?请充分说明理由.
解:
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:059
已知△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合).
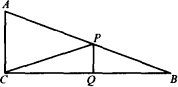
(1)如图所示,当PQ∥AC,且Q为BC的中点时,求线段CP的长;
(2)当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由.
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:059
在平面直角坐标系xOy中,已知A(4,0)、B(0,3),P是线段AB上一动点(与点A、B不重合),Q是线段OA上一动点(与点O、A不重合),C为OQ的中点,
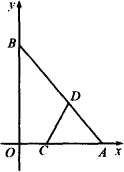
(1)求直线AB的解析式;
(2)过点C作AB的垂线,垂足为D,设OC=x,CD=d,写出d与x的函数关系式,并指出自变量x的取值范围;
(3)当OQ=3时,以OQ为直径作圆C,试判断直线AB与圆C的位置关系?
(4)当PQ不与x轴垂直时,△OPQ可能为直角三角形吗?若有可能,请求出线段OQ的长的取值范围,若不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com