
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第18期 总第174期 北师大版 题型:059
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、C两点的横坐标分别为1和4.
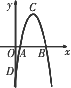
(1)求A、B两点的坐标;
(2)求二次函数的函数表达式;
(3)在(2)的抛物线上,是否存在点P,使得∠BAP=45°?若存在,求出点P的坐标及此时△ABP的面积;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第17期 总第173期 北师大版 题型:059
如图,抛物线l1:y=-x2-2x+3交x轴于A、B两点,交y轴于M点,抛物线l1向右平移2个单位得到抛物线l2,l2交x轴于C、D两点.
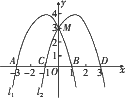
(1)求抛物线l2对应的函数表达式;
(2)抛物线l1或l2在x轴上方的部分是否存在点N,使以A、C、M、N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:重庆市开县中学2010届初三下学期“两考合一”模拟考试数学试题 题型:059
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥CB,点A坐标为(6,0),点B坐标为(3,4),点C在y轴的正半轴上,动点M在OA边上运动,从O点出发到A点;动点N在AB边上运动,从A点出发到B点,两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也就随即停止,设两点的运动时间为t(秒).
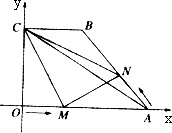
(1)求线段AB的长;并求当t为何值时,MN∥OC?
(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?
(3)连接CA,那么是否存在这样的t值,使MN与AC互相垂直?若存在,求出这时的t值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源:北京市顺义区2010届初三第一次统一练习数学试卷 题型:059
在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明.

(2)如图,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
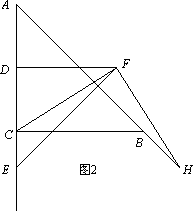
查看答案和解析>>
科目: 来源:浙江省东阳市2010届九年级5月学业水平考试数学试题 题型:059
如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
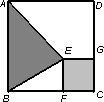
探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需________元;
探究2:如果木板边长为1米,求一块木板需用墙纸的最省费用;
探究3:设木板的边长为a(a为整数),当正方形EFCG的边长为多少时?墙纸费用最省;如要用这样的多块木板贴一堵墙(7×3平方米)进行装饰,要求每块木板A型的墙纸不超过1平方米,且尽量不浪费材料,则需要这样的木板________块.
查看答案和解析>>
科目: 来源:江苏省苏州太仓市2010届九年级质量调研测试数学试题 题型:059
在直角坐标系中以点P(1,-1)为圆心,2为半径作圆,交x轴于A、B两点,抛物线y=ax2+bx+c((a>0),过点A、B且顶点C在⊙O上.
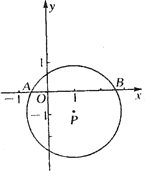
(1)求QP上劣弧AB的长;
(2)求抛物线的解析式,并在直角坐标系中画出草图;
(3)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:湖北省黄石市2010届九年级6月月考数学试题 题型:059
已知:直线y=2x+6与x轴和y轴交于点A、C两点,抛物线y=-x2+bx+c经过点A、C,点B是抛物线与x轴的另一个交点.

(1)求抛物线的表达式及点B的坐标;
(2)设点P时直线AC上的一点,且S⊿ABP∶S⊿BPC=1∶3,求点P的坐标.
(3)直线y=![]() x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由.
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源:广西贵港市教研室2010年中考教学质量监测调研数学试题(二) 题型:059
如图所示,直线y=-x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.

(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:江苏省姜堰市2010届九年级下学期期中考试数学试题 题型:059
已知抛物线y=-x2-2x+a(a>0)与y轴相交于点A,顶点为M直线y=![]() x+
x+![]() a与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
a与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
(1)求M的坐标与MA的解析式(用字母a表示),
(2)如图,将△NBC沿x轴翻折,若N点的对应点![]() 恰好落在抛物线上,求a的值
恰好落在抛物线上,求a的值
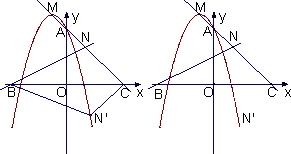
(3)在抛物线y=-x2-2x+a(a>0)上是否存在一点P,使得以P、B、C、N为顶点的四边形是平行四边形?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:江苏省苏州吴江市2010届初三上学期期末考试数学试题 题型:059
如图,已知:抛物线![]() 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是![]() ,连结AC.
,连结AC.

(1)B、C两点坐标分别为B(________,________)、C(________,________),抛物线的函数关系式为________;
(2)判断△ABC的形状,并说明理由;
(3)在△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com