
科目: 来源:江苏省南京三中2011届九年级上学期期末考试数学试题 题型:059
如图,点A、B在直线l上,AB=24 cm,⊙A、⊙B的半径开始都为2 cm,⊙A以2 cm/s的速度自左向右运动,设运动时间为t(s),自⊙A开始运动时,⊙B的半径不断增大,其半径r(cm)与时间t之间的关系式为r=2+t.
![]()
(1)写出点A、B之间的距离y(cm)与时间t之间的函数关系式;
(2)⊙A出发后多少秒两圆相切?
(3)当t=4时,⊙A停止向右运动,与此同时,⊙B的半径也不再增大,记直线l与⊙B左侧的交点为点C,将⊙A绕点C在平面内旋转360°.问:⊙A与⊙B能否相切?若能,请直接写出相切几次;若不能,请说明理由.
查看答案和解析>>
科目: 来源:湖北省黄冈市2011年春季八年级四科综合能力测评数学试题 题型:059
已知如图,动点P在反比例函数y=-![]() (x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
(x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;

(1)当点P的纵坐标为![]() 时,连OE,OF,求E、F两点的坐标及ΔEOF的面积;
时,连OE,OF,求E、F两点的坐标及ΔEOF的面积;
(2)动点P在函数y=-![]() (x<0)的图象上移动,它的坐标设为P(a,b)(-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
(x<0)的图象上移动,它的坐标设为P(a,b)(-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第12期 总第168期 沪科版 题型:059
如图,抛物线
y=-x2+bx+c与x轴、y轴分别相交于A(-1,0)、B(0,3)两点,其顶点为D.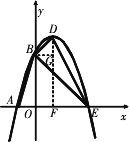
(1)求该抛物线的函数关系式;
(2)若该抛物线与x轴的另一个交点为E,求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第6期 总第162期 沪科版 题型:059
如图,在平面直角坐标系中,点
A、B的坐标分别为(-4,0)、(0,3).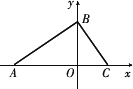
(1)求AB的长;
(2)过点B作BC⊥AB,交x轴于点C,求点C的坐标;
(3)在(2)的条件下,如果P、Q分别是AB和AC上的动点,连接PQ,设AP=CQ=m,问是否存在这样的m,使得△APQ与△ABC相似?若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第2期 总第158期 沪科版 题型:059
如图,抛物线
y=-x2-4x+5与x轴相交于点A、C,与y轴相交于点B,试问在抛物线的对称轴上是否存在一点P,使点P到点A、B的距离之和最短?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第25期 总第181期 北师大版 题型:059
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).
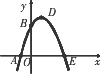
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给出证明;如果不相似,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第24期 总第180期 北师大版 题型:059
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第24期 总第180期 北师大版 题型:059
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.

(1)尺规作图:过A、D、C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A、D、C三点的圆的切线;
(3)若过A、D、C三点的圆的半径为![]() ,则线段BC上是否存在一点P,使得以P、D、B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P、D、B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第19期 总第175期 北师大版 题型:059
抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(3,0).
(1)求出一个符合上述条件的抛物线的解析式;
(2)若抛物线与y轴交于点C(0,![]() ),点E(x,y)是抛物线上位于x轴上方的一个动点,四边形OEBF是以OB为对角线的平行四边形.
),点E(x,y)是抛物线上位于x轴上方的一个动点,四边形OEBF是以OB为对角线的平行四边形.
①求□OEBF的面积S与x之间的函数关系式,当□OEBF的面积为![]() 时,求点E的坐标,并判断此时四边形OEBF是否为菱形?
时,求点E的坐标,并判断此时四边形OEBF是否为菱形?
②是否存在点E,使四边形OEBF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第19期 总第175期 北师大版 题型:059
阅读材料:
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC=![]() ah,即三角形面积等于水平宽与铅垂高乘积的一半.
ah,即三角形面积等于水平宽与铅垂高乘积的一半.
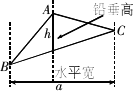
解答下列问题:
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
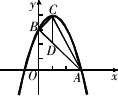
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连接PA、PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
(3)是否存在一点P,使S△PAB=![]() S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com