(2005　吉林)已知一抛物线形大门，其地面宽度AB=18m．一同学站在门内，在离门脚B点1m远的D处，垂直地面立起一根1.7m长的木杆，其顶端恰好顶在抛物线形门上C处，根据这些条件，请你求出该大门的高h．

(2005　河南)如图所示，正方形ABCD的边长为4cm，点P是BC边上不与B、C重合的任意一点，连接AP，过点P作PQ⊥AP交DC于点Q，设BP的长为x cm，CQ的长为y cm．

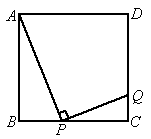
(1)求点P在BC上运动的过程中y的最大值；

(2)当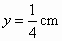时，求x的值．

(2005　江苏苏州)已知二次函数．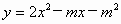

(1)求证：对于任意实数m，该二次函数图像与x轴总有公共点；

(2)若该二次函数图像与x轴有两个公共点A，B，且A点坐标为(1，0)，求B点坐标．

(2004　吉林)有一种葡萄，从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的个体重量基本保持不变．现有一个体户，按市场价收购了这种葡萄200kg放在冷藏室内，此时市场价为每千克2元，据测算，此后每千克鲜葡萄的价格每天可上涨0.2元，但是，存放一天需各种费用20元，日平均每天还有1kg葡萄变质丢弃．

(1)设x天后每千克鲜葡萄的市场价为P元，写出P关于x的函数关系式；

(2)若存放x天后将鲜葡萄一次性出售，该鲜葡萄的销售总金额为y元，写出y关于x的函数关系式；

(3)该个体户将这批葡萄存放多少天后出售，可获最大利润Q？最大利润Q是多少？(本题不要求写出自变量的取值范围)．

(2005　青岛)在青岛市开展的创城活动中，某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，图所示．若设花园的BC边长为x m，花园的面积为．

(1)求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)满足条件的花园面积能达到吗？若能，求出此时x的值；若不能，请说明理由；

(3)根据(1)中求得的函数关系式，描述其图像的变化趋势；并结合题意判断当x取何值时，花园的面积最大？最大面积为多少？

(2005　南京)在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子．镜子的长与宽的比是2∶1．已知镜面玻璃的价格是每平方米120元，边框的价格是每米20元，另外制作这面镜子还需加工费45元．设制作这面镜子的总费用是y元，镜子的宽度是x m．

(1)求y与x之间的关系式；

(2)如果制作这面镜子共花了165元，求这面镜子的长和宽．

(2005　湖北武汉)如图所示，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系．y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．

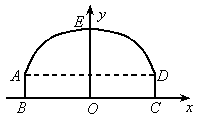
(1)求抛物线的解析式；

(2)如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4m，这辆货运卡车能否通过该隧道？过计算说明你的结论．

(2005　河南)已知一个二次函数的图像过如图所示三点．

(1)求抛物线的对称轴；

(2)平行于x轴的直线l的解析式为，抛物线与x轴交于A、B两点，在抛物线的对称轴上找点P，使BP的长等于直线l与x轴间的距离．求点P的坐标．

(2005　安徽芜湖)已知二次函数图像经过(2，－3)，对称轴x=1，抛物线与x轴的两个交点距离为4，求这个二次函数的解析式．

(2006北京课改，21)在平面直角坐标系xOy中，直线y=－x绕点O顺时针旋转90°得到直线l．直线l与反比例函数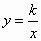的图象的一个交点为A(a，3)，试确定反比例函数的解析式．