
科目: 来源: 题型:044
(2006,南充)已知A(0,-6)、B(-3,0)、C(m,2)三点在同一直线上,试求出图象经过其中一点的反比例函数的解析式并画出其图象.(要求标出必要的点,可不写画法)

查看答案和解析>>
科目: 来源: 题型:044
(2006,德州非课改)如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.
(1)如果∠BAC=30°,∠=DAE=105°,试确定y与x之间的函数关系式;
(2)如果∠BAC的度数为α,∠DAE的度数为β,当α,β满足怎样的关系式时,(1)中y与x之间的函数关系式还成立,试说明理由.
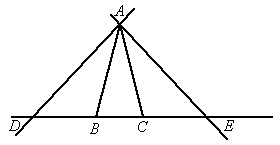
查看答案和解析>>
科目: 来源: 题型:044
(2005·广东佛山)“三等分角”是数学史上一个著名问题,但仅用标尺不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图所示):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数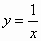 的图像交于点P,以P为圆心、以2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的并行线,两直线相交于点M,连接OM得到∠MOB,则
的图像交于点P,以P为圆心、以2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的并行线,两直线相交于点M,连接OM得到∠MOB,则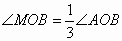 .要明白帕普斯的方法,请研究以下问题:
.要明白帕普斯的方法,请研究以下问题:
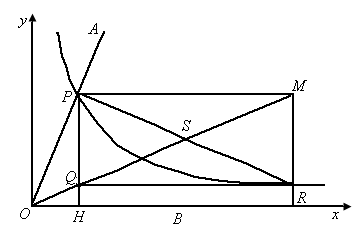
(1)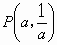 、
、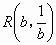 ,求直线OM对应的函数表达式(用a、b的代数式表示);
,求直线OM对应的函数表达式(用a、b的代数式表示);
(2)分别过点P和R作y轴和x轴的并行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明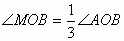 ;
;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明).
查看答案和解析>>
科目: 来源: 题型:044
将图中△ 作下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.
作下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.
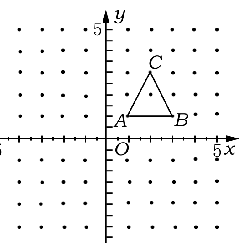
(1)关于 轴对称;
轴对称;
(2)沿 轴反向平移3个单位;
轴反向平移3个单位;
(3)以 点为位似中心,缩小1倍.
点为位似中心,缩小1倍.
查看答案和解析>>
科目: 来源: 题型:044
一个口袋装有大小相等的白、红、黑三种颜色的小球.其中白球1只,红球3只,黑球5只.
随机地从袋中取出1只球,(用分数表示)
(1)求取出的球是白球的概率是______
(2)求取出的球是红球的概率是______
(3)求取出的球是黑球的概率是______
若取出的第1只球是红球,将它放在桌上,从袋中余下的球中再随机地取出1球,这时
(4)求取出的球是白球的概率是______
(5)求取出的球是红球的概率是______
(6)求取出的球是黑球的概率是______
若取出的第1只球是白球,将它放在桌上,从袋中余下的球中再随机地抽取出1球,这时
(7)取出白球概率又是______
(8)取出红球概率又是______
(9)取出黑球概率又是______
查看答案和解析>>
科目: 来源: 题型:044
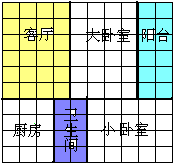
小偷进入一户家庭行窃,若每次他都停留在一块地砖上(所有地砖都一样,如图),则
(1)小偷留在哪个房间内的概率最大.
(2)分别计算小偷停留在6个房间内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com