(2006河北课改，24)(12分)利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，求售出的由厂家负责处理)．当每吨售价为260元时，月销售量为45吨，该经销店为提高经营利润，准备采取降价的方式进行促销．经市场发现，当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其他费用100元，设每吨材料售价为x(元)，该经销店的月利润为y(元)．

(1)当每吨售价是240元时，计算此时的月销售量；

(2)求出y与x的函数关系式(不要求写出x的取值范围)；

(3)该经销店要获得最大月利润，售价应定为每吨多少元？

(4)小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．

(2006安徽课改，21)抛物线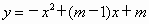与y轴交于(0，3)点．

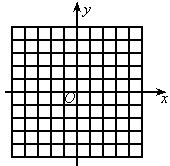
(1)求出m的值并画出这条抛物线；

(2)求它与x轴的交点和抛物线顶点的坐标；

(3)x取什么值时，抛物线在x轴上方？

(4)x取什么值时，y的值随x值的增大而减小？

(2006湖北武汉课改，23)(10分)连接着汉口集家咀和汉阳南岸咀的江汉三桥(晴川桥)，是一座下承式钢管混凝土系杆拱桥．它犹如一道美丽的彩虹跨越汉江，是江城武汉的一道靓丽景观．桥的拱肋ACB视为抛物线的一部分，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，相邻系杆之间的间距均为5米(不考虑系杆的粗细)，拱肋的跨度AB为280米，距离拱肋的右端70米处的系杆EF的长度为42米．以AB所在直线为x轴，抛物线的对称轴为y轴建立如图2所示的平面直角坐标系．

(1)求抛物线的解析式；

(2)正中间系杆OC的长度是多少米？是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．

(2006，长沙)如图1，已知直线与抛物线交于A、B两点．

(1)求A、B两点的坐标；

(2)求线段A、B的垂直平分线的解析式；

(3)如图2，取与线段AB等长的一根橡皮筋，端点分别固定在A、B两处．用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动，动点P将与A、B构成无数个三角形，这些三角形中是否存在一个面积最大的三角形?如果存在，求出最大面积，并指出此时P点的坐标；如果不存在，请简要说明理由．

(2006，荆州)荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜，通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌设备，这项费用(万元)与大棚面积(公顷)的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元．每公顷蔬菜年平均可卖7.5万元．

(1)基地的菜农共修建大棚x(公顷)，当年收益(扣除修建和种植成本后)为y(万元)，写出y关于x的函数关系式；

(2)若某菜农期望通过种植大棚蔬菜当年获得5万元收益，工作组应建议他修建多少公顷大棚?(用分数表示即可)

(3)除种子、化肥、农药投资只能当年受益外，其他设施3年内不需增加投资仍可继续使用．如果按3年计算，是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议．

(2006，吉林)如图，三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度AB=20m，顶点M距水面6m(即MO=6m)，小孔顶点N距水面4.5m(即NC=4.5m)．当水位上涨刚好淹没小孔时，借助图中的直角坐标系，求此时大孔的水面宽度EF．

(2006，杭州)杭州体博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收33万元．而该游乐设施开放后，从第1个月到第x个月的维修保养费用累计为y(万元)，且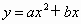；若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元)，g也是关于x的二次函数．

(1)若维修保养费用第1个月为2万元，第2个月为4万元，求y关于x的解析式；

(2)求纯收益g关于x的解析式；

(3)设施开放几个月后，游乐场的纯收益达到最大?几个月后，能收回投资?

(2006，济南)某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱．如图(1)，废纸箱的一面利用墙，放置在地面上，利用地面作底，其他的面用一张边长为60cm的正方形硬纸板围成．经研究发现：由于废纸箱的高是确定的，所以废纸箱的横截面图形面积越大，则它的容积越大．

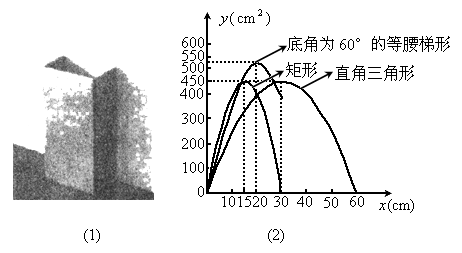
(1)该小组通过多次尝试，最终选定下表中的简便且易操作的三种横截面图形，如图(2)，是根据这三种横截面图形的面积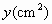与x(cm)(见表中横截面图形所示)的函数关系式而绘制出的图象．请你根据有关信息，在表中空白处填上适当的数、式，并完成y取最大值时的设计示意图；

(2)在研究性学习小组展示研究成果时，小华同学指出：图(2)中“底角为60°的等腰梯形”的图象与其他两个图象比较，还缺少一部分，应该补画．你认为他的说法正确吗?请简要说明理由．

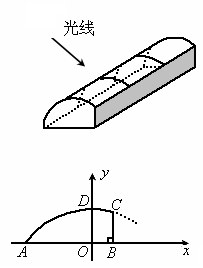
(2006，武汉)某塑料大棚的截面如图所示，曲线部分近似看作抛物线．现测得AB=6m，最高点D到地面AB的距离DO=2.5m，点O到墙BC的距离OB=1m．借助图中的直角坐标系，回答下列问题：

(1)写出点A、B的坐标；

(2)求墙高BC．

(2006，武汉)连接着汉口集家嘴的江汉三桥(晴川桥)是一座下承式钢管混凝土系杆拱桥，它犹如一道美丽的彩虹跨越汉江，是江城武汉的一道靓丽景观．桥的拱肋ACB视为抛物线的一部分，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，相邻系杆之间的间距均为5m(不考虑系杆的粗细)，拱肋的跨度AB为280m，距离拱肋的右端70m处的系杆EF的长度为42m，以AB所在直线为x轴，抛物线的对称轴为y轴建立如图所示的平面直角坐标系．

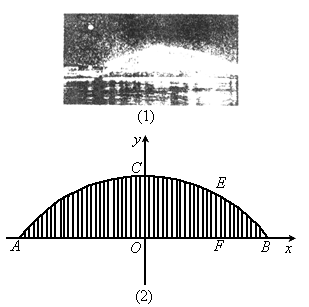
(1)求抛物线的解析式；

(2)正中间系杆OC的长度是多少米?是否存在一根系杆的长度恰好是OC长度的一半?请说明理由．