
科目: 来源: 题型:044
(2004青岛课改)把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角形板EFG绕O点按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
|
图① |
图② |
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的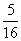 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(2006黑龙江课改,26)(8分)已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD到OA垂直时(如图1),易证 .
.

图1
当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?
|
图2 |
图3 |
查看答案和解析>>
科目: 来源: 题型:044
(2006 湖南)如图1,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较小直角边的长为6cm,较小锐角的度数为30°.
(1)将△ECD沿直线AC翻折到图2的位置,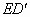 与AB相交于点F,请证明:
与AB相交于点F,请证明: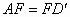 .
.
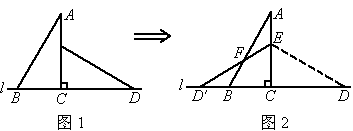
(2)将△ECD沿直线l向左平移到图10(b)的位置,使E点落在AB上,你可以求出平移的距离,试试看;
(3)将△ECD绕点C逆时针方向旋转到图10(c)的位置,使E点落在AB直,请求出旋转角的度数.
|
(b) |
(c) |
查看答案和解析>>
科目: 来源: 题型:044
(2005·南京)在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角.例如:正方形绕着它的对角线的交点旋转90°后能与自身重合(如图所示),所以正方形是旋转对称图形,它有一个旋转角为90°.

(1)判断下列命题的真假(在相应的括号内填上“真”或“假”).
①等腰梯形是旋转对称图形,它有一个旋转角为180°.
( )
②矩形是旋转对称图形,它有一个旋转角为180°.
( )
(2)填空:下列图形中,是旋转对称图形,且有一个旋转角为120°的是________(写出所有正确结论的序号)①正三角形;②正方形;③正六边形;④正八边形.
(3)写出两个多边形,它们都是旋转对称图形,都有一个旋转角为72°,并且分别满足下列条件:
①是轴对称图形,但不是中心对称图形:________;
②既是轴对称图形,又是中心对称图形:________.
查看答案和解析>>
科目: 来源: 题型:044
(2003江苏徐州)如图,正方形ABCD和正方形EFGH的边长分别为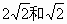 ,对角线BD、FH都在直线l上,
,对角线BD、FH都在直线l上,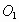 、
、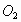 分别为正方形的中心,线段
分别为正方形的中心,线段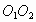 的长叫做两个正方形的中心距,当中心
的长叫做两个正方形的中心距,当中心 在直线l上平移时,正方形EFGH也随之平移,在平移时,正方形EFGH的形状、大小没有变化.
在直线l上平移时,正方形EFGH也随之平移,在平移时,正方形EFGH的形状、大小没有变化.
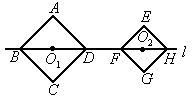
(1)计算: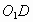 =________,
=________,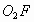 =________;
=________;
(2)当中心 在直线l上平移到两个正方形只有一个公共点时,中心距
在直线l上平移到两个正方形只有一个公共点时,中心距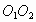 =________;
=________;
(3)随着中心 的在直线l上平移,两个正方形的公共点的个数还有哪些变化?并求相对应的中心距的值或取值范围(不必写出计算过程).
的在直线l上平移,两个正方形的公共点的个数还有哪些变化?并求相对应的中心距的值或取值范围(不必写出计算过程).
查看答案和解析>>
科目: 来源: 题型:044
(2006重庆课改,28)(10分)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成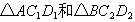 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片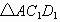 沿直线
沿直线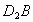 (AB)方向平移(点A,
(AB)方向平移(点A,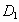 ,
, ,B始终在同一条直线上),当点
,B始终在同一条直线上),当点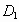 与点B重合时,停止平移.在平移的过程中,
与点B重合时,停止平移.在平移的过程中,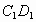 与
与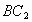 交于点E,
交于点E,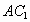 与
与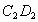 、
、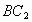 分别交于点F、P.
分别交于点F、P.
|
图1 |
图2 |
(1)当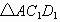 平移到如图3所示的位置时,猜想图中
平移到如图3所示的位置时,猜想图中 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
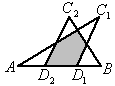
图3
(2)设平移距离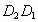 为x,
为x,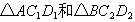 重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
(3)对于(2)中结论是否存在这样的x,使得重叠部分面积等于原△ABC纸片面积的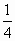 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(2004·河北鹿泉)如图所示,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网格的底部重合时,继续以同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动,设运动时间为x秒,△QAC的面积为y.
(1)如图所示,当Rt△ABC向下平移到 的位置时,请你在网格图中画出
的位置时,请你在网格图中画出 关于直线QN成轴对称的图形;
关于直线QN成轴对称的图形;

(2)如图所示,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?

(3)在Rt△ABC向右平移的过程中,请你说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?为什么?
查看答案和解析>>
科目: 来源: 题型:044
(2007,长沙,23)小华准备将平时的零用钱节约一些储存起来,他已存有62元,从现在起每个月存12元;小华的同学小丽以前没有存过零用钱,听到小华在存零用钱,表示从现在起每个月存20元,争取超过小华.
(1)试写出小华的存款总数 与从现在开始的月数x之间的函数关系式以及小丽存款数
与从现在开始的月数x之间的函数关系式以及小丽存款数 与月数x之间的函数关系式;
与月数x之间的函数关系式;
(2)从第几个月开始小丽的存款数可以超过小华?
查看答案和解析>>
科目: 来源: 题型:044
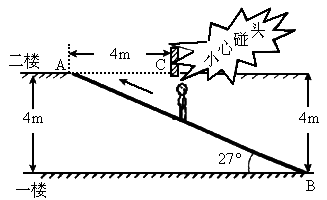
(2007,长沙,22)如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
(可能用到的参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)
查看答案和解析>>
科目: 来源: 题型:044
(2007,河南,21)请你画出一个以BC为底边的等腰△ABC,使底边上的高AD=BC.
(1)求tanB和sinB的值;
(2)在你所画的等腰△ABC中,假设底边BC=5米,求腰上的高BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com