
科目: 来源: 题型:044
(2007,辽宁省大连市,24)已知抛物线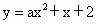 .
.
(1)当a=-1时,求此抛物线的顶点坐标和对称轴;
(2)若代数式 的值为正整数,求x的值;
的值为正整数,求x的值;
(3)当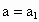 时,抛物线
时,抛物线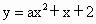 与x轴的正半轴相交于点M(m,0);当
与x轴的正半轴相交于点M(m,0);当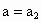 时,抛物线
时,抛物线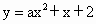 与x轴的正半轴相交于点N(n,0).若点M在点N的左边,试比较
与x轴的正半轴相交于点N(n,0).若点M在点N的左边,试比较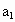 与
与 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:044
(2007,兰州,30)已知抛物线 的图像交x轴于点A(
的图像交x轴于点A( ,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D.
,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D.
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M、N两点,以MN为一边,抛物线上任一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式.
(4)当 时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(2007,山西,26)关于x的二次函数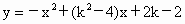 以y轴为对称轴,且与y轴的交点在x轴上方.
以y轴为对称轴,且与y轴的交点在x轴上方.
(1)求此抛物线的解析式,并在下面的直角坐标系中画出函数的草图;
(2)设A是y轴右侧抛物线上的一个动点,过点A作AB垂直于x轴于点B,再过点A作x轴的平行线交抛物线于点D,过点D作DC垂直于x轴于点C,得到矩形ABCD.设矩形ABCD的周长为l,点A的横坐标为x,试求l关于x的函数关系式;
(3)当点A在y轴右侧的抛物线上运动时,矩形ABCD能否成为正方形.若能,请求出此时正方形的周长;若不能,请说明理由.
参考资料:抛物线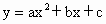 (a≠0)的顶点坐标是(
(a≠0)的顶点坐标是(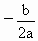 ,
,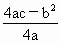 ),对称轴是直线
),对称轴是直线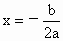 .
.
查看答案和解析>>
科目: 来源: 题型:044
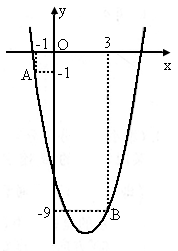
(2007,河北,22)如图,已知二次函数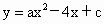 的图像经过点A和点B.
的图像经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
查看答案和解析>>
科目: 来源: 题型:044
(2007,重庆,28)解答时必须给出必要的演算过程或推理步骤.
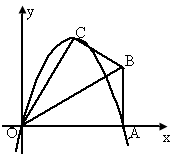
已知,在Rt△OAB中,∠OAB=90°.∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线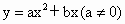 经过C、A两点,求此抛物线的解析式;
经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(注:抛物线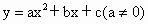 的顶点坐标为(
的顶点坐标为( ,
, ),对称轴公式为
),对称轴公式为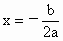 )
)
查看答案和解析>>
科目: 来源: 题型:044
(2007,北京,24)在平面直角坐标系xOy中,抛物线 经过P(
经过P( ,5),A(0,2)两点.
,5),A(0,2)两点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为B,将直线AB沿y轴向下平移两个单位得到直线l,直线l与抛物线的对称轴交于C点,求直线l的解析式;
(3)在(2)的条件下,求到直线OB、OC、BC距离相等的点的坐标.

查看答案和解析>>
科目: 来源: 题型:044
(2005 烟台)如图所示,在平面直角坐标系中,以点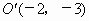 为圆心,5为半径的圆交x轴于A、B两点,过点B作
为圆心,5为半径的圆交x轴于A、B两点,过点B作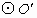 的切线,交y轴于点C,过点
的切线,交y轴于点C,过点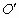 作x轴的垂线MN,垂足为D,一条抛物线(对称轴与y轴平行)经过A、B两点,且顶点在直线BC上.
作x轴的垂线MN,垂足为D,一条抛物线(对称轴与y轴平行)经过A、B两点,且顶点在直线BC上.
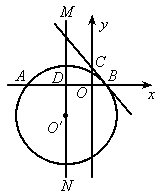
(1)求直线BC的解析式;
(2)求抛物线的解析式;
(3)设抛物线与y轴交于点P,在抛物线上是否存在一点Q,使四边形DBPQ为平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(2003 吉林省)如图所示,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
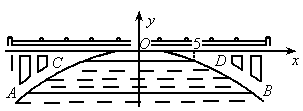
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以40km/h的速度开往乙地,当行驶1h时,忽然接到紧急通知:前方连降暴雨,造成水位以0.25m/h的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行).试问:如果货车按原来的速度行驶,能否安全通过此桥?若能,请说明理由.若不能,货车在接到通知后立即提速,要使货车完全通过此桥,那么提速后速度应超过每小时多少千米?
查看答案和解析>>
科目: 来源: 题型:044
(2005 海南)如图所示,抛物线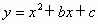 与x轴交于A(-1,0)、B(3,0)两点.
与x轴交于A(-1,0)、B(3,0)两点.
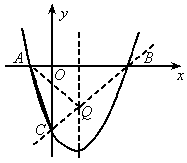
(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足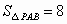 ,并求出此时P点的坐标;
,并求出此时P点的坐标;
(3)设(1)中的抛物线交y轴于C点.在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(2005 湖北黄冈)在黄州服装批发市场,某种品牌的时装当季节即将来临时,价格呈上升趋势.设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售.
(1)试建立销售价y与周次x之间的函数关系式;
(2)若这种时装每件进价Z与周次x之间的关系为Z=-0. ,1≤x≤16,且x为整数,试问该服装第几周出售时,每件销售利润最大?最大利润是多少?
,1≤x≤16,且x为整数,试问该服装第几周出售时,每件销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com