
科目: 来源: 题型:044
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:
请根据以下图案回答问题:(1)在图①中,如果铝合金材料总长度(图中所有黑线的长度和)为6 m,当AB为1 m时,长方形框架ABCD的面积是_________
(2)
在图②中,如果铝合金材料总长度为6 m,设AB为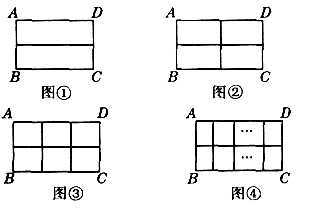
(3)
经过这三种情形的试验,他们发现对于图④这样的情形也存在着一定的规律.那么这个规律是什么?请加以证明
查看答案和解析>>
科目: 来源: 题型:044
东方专卖店专销某种品牌的计算器,进价12元/只,售价20元/只.为了促销,专卖店决定凡是买10只以上的,每多买一只,售价就降价0.10元[例如,某人买20只计算器,于是每只降价![]() 元,就可以按19元/只的价格购买,但是最低价为16元/只.
元,就可以按19元/只的价格购买,但是最低价为16元/只.
(1)
求顾客一次至少买多少只,才能以最低价购买?(2)
写出当一次购买(3)
有一天,一位顾客买了46只,另一位顾客买了50只,专卖店发现卖了50只反而比卖46只赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元/只至少要提高到多少?为什么?查看答案和解析>>
科目: 来源: 题型:044
如图,一位篮球运动员跳起投篮,球沿抛物线![]() 运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
(1)
球在空中运行的最大高度为多少米?(2)
如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
查看答案和解析>>
科目: 来源: 题型:044
如图,面积为18的等腰△OAB的一条直角边OA在![]() 轴上,二次函数
轴上,二次函数![]() 的图象过原点、A点和斜边OB的中点M.
的图象过原点、A点和斜边OB的中点M.
(1)求出这个二次函数的关系式和对称轴;
(2)
在坐标轴上是否存在一点P,使△PMA中PM=PA?若存在,写出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:044
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.
求证:△ABC≌△A1B1C1.
(
请你将下列证明过程补充完整)证明:分别过点B,B1作BD⊥CA于D,
B
1 D1⊥C1 A1于D1.则∠BDC=∠B1D1C1=900,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
(2)
归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.
查看答案和解析>>
科目: 来源: 题型:044
下表是某市2004年城市居民收支情况抽样调查表,阅读表内信息,完成以下问题.

(1)
说明该市城市居民可支配收入的主要来源是 收入;(2)
该市城市居民可支配收入中同比增长最快的是 收入;(3)
从该市城市居民在消费支出方面的信息,你能得出哪些结论?试写出其中的两条 .查看答案和解析>>
科目: 来源: 题型:044
按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(
Ⅰ)新数据都在60~100(含60和100)之间;(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。(1)
若y与x的关系是y=x+p(100-x),请说明:当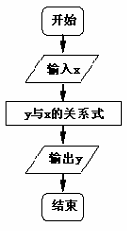
查看答案和解析>>
科目: 来源: 题型:044
如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.

(1)
在如图的坐标系中求抛物线的解析式;(2)
若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?查看答案和解析>>
科目: 来源: 题型:044
在边长为6 cm的正方形ABCD中,点E、F、G、H分别按A→B、B→C、C→D、D→A的方向同时出发,以1 cm/s的速度匀速运动.

(1)
在运动中,点E、F、G、H所形成的四边形EFGH为( )A
.平行四边形 B.矩形 C.菱形 D.正方形(2)
四边形EFGH的面积S(cm2)随运动时间t(s)变化的图象大致是( )

(3)
写出四边形EFGH的面积S(cm2)关于运动时间t(s)变化的函数关系式,并求运动几秒钟时,面积最小?最小值是多少?查看答案和解析>>
科目: 来源: 题型:044
已知:c<0,且满足![]()
![]() 抛物线
抛物线![]() 经过正比例函数
经过正比例函数![]() 与反比例函数
与反比例函数![]() 的图像的交点.
的图像的交点.
(1)
求抛物线的解析式;(2)
若抛物线顶点在直线查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com