某商场为吸引消费者，推出一种食品的有奖销售方法：每袋食品中装有一张小卡片，每张卡片上写着一个字，分别是撟?、撃銛、摵脭、撛藬，如能集齐不同的四个字，则可领取奖品一份，假定厂商在包装时放入袋中的四种卡片总张数相同，请你设计一个实验来估计买五袋食品即可中奖的机会。

(1)如图所示的转盘中指针落在每个数字上的机会相等，现同时转动A、B两转盘，停止后，指针各指向一个数字，小彬和小颖利用这个转盘做游戏：若两数之积为非负数则小彬胜，否则，小颖胜．你认为这个游戏对双方公平吗？______(直接写出结果)．

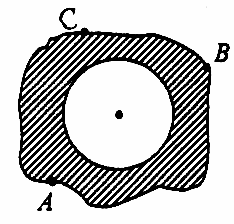
(2)小明在操场上做游戏，他发现地上有一个不规则的封闭图形ABC．为了知道它的面积，小明在封闭图形内划出了一个半径为1米的圆，如图，在不远处向圈内掷石子，且记录如下：

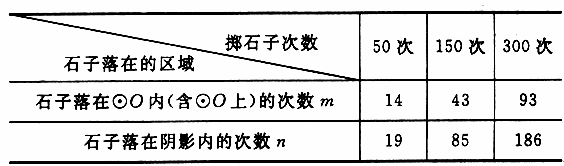
你能否求出封闭图形ABC的面积？试试看．

某商场为了吸引顾客，规定：凡购买200元以上物品的顾客均可获奖，可以直接获得购物券10元，也可以参加摸奖．摸奖的具体方法是：从一个装有100个彩球的盒子中任取一球，摸到红球可获100元的购物券．摸到黄、蓝球，可分别获得50元、20元的购物券，而摸到白球，不能获奖．已知100个球中，5个红球，10个黄球，20个蓝球，其余均为白球．现有一名顾客可以直接获购物券10元，也可参加摸奖一次，请你帮他选择，哪种方式更合算？

阅读以下材料并完成问题．

平面上有n个点(n≥2)，且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？

①分析：当仅有两个点时，可连成1条直线；

当有3个点时，可连成3条直线；

当有4个点时，可连成6条直线；

当有5个点时，可连成10条直线；

②归纳：考查点的个数n和可连成直线的条数，发现：

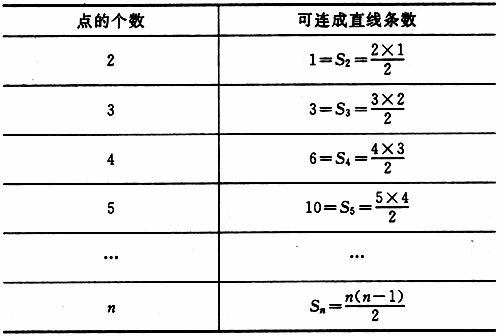
③推理：平面上有n个点，两点确定一条直线，取第一个点A有n种取法，取第二个点B有(n-1)种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2，即

④结论：

试探究以下问题：

平面上有n(n≥3)个点，任意三个点不在同一直线上，过任意三点作三角形一共能作出多少不同的三角形？

(1)分析：当仅有3个点时，可作______个三角形；当有4个点时，可作______个三角形；当有5个点时，可作______个三角形，

(2)归纳：考查点的个数n和可作出的三角形的个数发现：

(3)推理：______________________________________

(4)结论：______________________________________

数学家高斯在读小学二年级时老师出了这样一道计算题：

1+2+3+4+…+100=?

高斯很快得出了答案，他的计算方法是：

1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×(1+100)=5050．

(1)请你应用上述方法求S=1+3+5+…+(2n-1)的计算公式；

(2)如图，第二个图形是由第一个图形中的三角形连接三边中点而得到的，第三个图形是第二个图形中间一个三角形连结三边中点而得到的，依此类推……

分别写出第二个图形、第三个图形和第四个图形的三角形的个数，由此推测出第n个图形中三角形的个数，并求出第一个图形到第n个图形的三角形个数之和S．

1953年第一次人口普查我国人口总数为60194万人，2000年第五次人口普查我国人口总数为129533万人，2000年天津市人口1001万人，那么我国每年相当于新增加多少个天津市人口？

一个盒子中有若干双黑袜子，没有其他颜色的袜子，不允许将袜子倒出来数，你能设计一个方案估计其中的袜子数吗?

为了研究某个地区的生态状况，生物工作者往往需要估计这一地区各种生物的数量，你能设计一个方案，估计山林中猴子的数目吗?

为估计某草原天鹅湖中天鹅的数量，先捕捉10只，全部做上标记后放飞，过一段时间后，重新捕捉40只，数一数带有标记的天鹅有2只，据此可估算出该地区大约有天鹅多少只?

一个袋子里有10个黑球和若干个白球，从袋子里摸出10个球，记录下黑球的个数，再放回去摇匀，重复这样的试验20次，共摸出黑球18个，则估算袋中共有白球的个数．