某跳水运动员进行10m跳台跳水训练，身体(将运动员看成一点)在空中运动的路线是如图所示坐标系经过原点O的抛物线(图中标出的数据为已知数据)．在跳某个规定动作时，正常情况下，该运动员在空中最高处距水面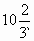m，入水处距池边4m，同时运动员在距水面高度5m以前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误．

(1)求这条抛物线的关系式；

(2)某次试跳中，测得运动员在空中的运动路线是(1)中的抛物线，且运动员在空中调整好入水姿势时池边的水平距离为m，问此次跳水会不会失误？通过计算说时理由．

某商场购进一批单价为16元的日用品，销售一段时间后，为了获得更多利润，商店决定提高销售价格．经试验发现，若按每件20元的价格销售时，每月能卖300件，若按件25元的价格销售时，每月能卖210件，假定每月销售件数y(件)是价格x(元/件)的一次函数．

(1)试求y与x之间的函数关系式；

(2)在商品不积压，且不考虑其他因素的前提下，问销售价格定为多少时，才能使每月获得最大利润？每月的最大利润是多少？(总利润=总收入－总成本)

已知抛物线．

(1)证明：此抛物线与x轴总有两个不同的交点；

(2)a取何值时，两点间的距离最小？

已知：二次函数

(1)求证：二次函数的图像和x轴总有公共点．

(2)若此图像和x轴有两个公共点A、B且A(1，0)．求B点坐标．

某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米l000元．设矩形一边长为x米，面积为S平方米．

(1)求出S与x之间的函数关系式，并确定自变量x的取值范围；

(2)请你设计一个方案，使获得的设计费最多，并求出这个费用．

某商场销售某种品牌的纯牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40元～70元之间．市场调查发现：若每箱以50元销售，平均每天销售90箱；价格每降底l元，平均每天多销售3箱；价格每升高1元，平均每天少销售3箱．

(1)写出平均每天销售量y(箱)与每箱售价x(元)之间的函数关系式；

(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式；(每箱的利润＝售价一进价)

(3)求出(2)中二次函数图像的顶点坐标，并求当x＝40，70时W的值，在给出的坐标系(如图)中画出函数的草图；

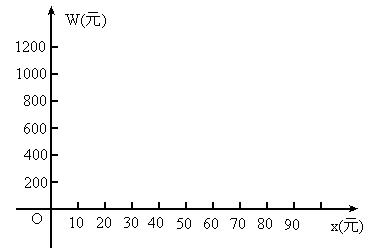
(4)由函数图像可以看出，当牛奶售价为多少时，平均每天的利润最大?最大利润为多少?

某电影院设有1000个座位，门票每张3元可达客满．据市场估计，若每张票价提高x元，将有200x张门票不能售出．

(1)求提价后每场电影的票房收入y(元)与票价提高量x(元)之间的函数关系式和自变量x的取值范围；

(2)为增加收益，电影院应做怎样的决策(提价还是不提价)?若提价，提价多少为宜?

某工厂生产A产品x吨所需费用为P元，而卖出x吨这种产品的售价为每吨Q元．己知．

(1)该厂生产并售出x吨，写出这种产品所获利润W(元)关于x(吨)的函数关系式；

(2)当生产多少吨这种产品，并全部售出时，获利最多?这时获利多少元?这时每吨的价格又是多少元?

如图所示，E、F分别是边长为4的正方形ABCD的边BC、CD上的点，CE=1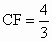，．直线FE交AB的延长线于G，过线段FG上的一个动点H作HM⊥AG，HN⊥AD，垂足分别为M、N．

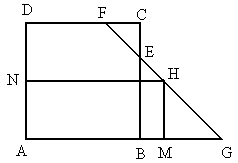
设HM=x，矩形AMHN的面积为y．

(1)求y与x之间的函数关系式；

(2)当x为何值时，矩形AMHN的面积最大？最大面积是多少？

有一条长7.2米的木料，做成如图所示的“日”字形的窗框，问窗框的高和宽各取多少米时，这个窗的面积最大？(不考虑木料加工时损耗和中间木框所占的面积)