
科目: 来源:数学教研室 题型:044
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽度是10m.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计),货车正以每小时40km的速度开往乙地,当行驶1h时,忽然接到紧急通知,前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位到达拱桥最高点O时,禁止车辆通行).试问:如果货车按原来的速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,车速应超过每小时多少千米?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
某公司生产的A种产品,每件的成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告,根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数.公司做了预测,得知x与y之间的对应
关系如下表:
|
x(万元) |
0 |
1 |
2 |
.... |
|
y |
1 |
1.5 |
1.8 |
... |
(1)根据上表,求y关于x的函数关系式.
(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润W(万元)与广告费x(万元)的函数关系式.
(3)从上式的函数关系式中,你能得出什么结论?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
有一种螃蟹,从海上捕获后,如果不放养的话最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体重量基本保持不变.现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时市场价为每千克30元.据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元.
(1) 设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式。
(2) 如果放养x天后将活蟹一次性售出,并记1000千克蟹的销售总额为Q 元,写出Q关于x的函数关系式。
(3) 该经销商将这批蟹放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用)?最大利润是多少?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
某化工厂材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元,物价部门规定其销售价不高于每千克70元,也不能低于30元,市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多销2千克,在销售过程中,每天还要支出其他费用500元,设销售单价为x元,日均获利y元.
(1)求y关于x的函数关系式.
(2)求出单价多少时,日获利最多,是多少?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
已知抛物线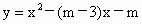 .
.
(1)试证:无论m为任何值,抛物线与x轴总有两个交点;
(2)问:m为何值时,抛物线与x轴的两个交点的距离等于3?
(3)探索:抛物线与x轴的两个交点能否都落在x轴的正半轴上?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
如图所示,舞台的左上角和右上角分别吊有灯泡M、N,灯高9.6m,身高均为1.6m的甲、乙两演员分别站在舞台的P、Q处,此时,灯M对乙的影子的顶部正好落在灯N的正方,灯N对甲的影子的顶部也正落在灯M的正下方,甲,乙两演员相距6m,求舞台AB宽.
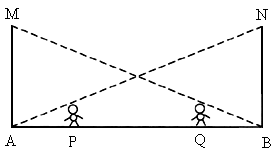
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com