某公司生产的A种产品，每件的成本是2元，每件售价是3元，一年的销售量是10万件．为了获得更多的利润，公司准备拿出一定资金来做广告，根据经验，每年投入的广告费为x(万元)时，产品的年销售量是原来的y倍，且y是x的二次函数．公司做了预测，得知x与y之间的对应

关系如下表：

(1)根据上表，求y关于x的函数关系式．

(2)如果把利润看成是销售总额减去成本和广告费，请你写出年利润W(万元)与广告费x(万元)的函数关系式．

(3)从上式的函数关系式中，你能得出什么结论？

有一种螃蟹，从海上捕获后，如果不放养的话最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去．假设放养期内蟹的个体重量基本保持不变．现有一经销商，按市场价收购了这种活蟹1000千克放养在塘内，此时市场价为每千克30元．据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需各种费用支出400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克20元．

(1) 设x天后每千克活蟹的市场价为P元，写出P关于x的函数关系式。

(2) 如果放养x天后将活蟹一次性售出，并记1000千克蟹的销售总额为Q 元，写出Q关于x的函数关系式。

(3) 该经销商将这批蟹放养多少天后出售，可获最大利润（利润=销售总额-收购成本-费用）？最大利润是多少？

某化工厂材料经销公司购进了一种化工原料共7000千克，购进价格为每千克30元，物价部门规定其销售价不高于每千克70元，也不能低于30元，市场调查发现：单价定为70元时，日均销售60千克；单价每降低1元，日均多销2千克，在销售过程中，每天还要支出其他费用500元，设销售单价为x元，日均获利y元．

(1)求y关于x的函数关系式．

(2)求出单价多少时，日获利最多，是多少?

已知抛物线．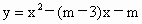

(1)试证：无论m为任何值，抛物线与x轴总有两个交点；

(2)问：m为何值时，抛物线与x轴的两个交点的距离等于3？

(3)探索：抛物线与x轴的两个交点能否都落在x轴的正半轴上？

某跳水运动员进行10m跳台跳水训练，身体(将运动员看成一点)在空中运动的路线是如图所示坐标系经过原点O的抛物线(图中标出的数据为已知数据)．在跳某个规定动作时，正常情况下，该运动员在空中最高处距水面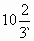m，入水处距池边4m，同时运动员在距水面高度5m以前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误．

(1)求这条抛物线的关系式；

(2)某次试跳中，测得运动员在空中的运动路线是(1)中的抛物线，且运动员在空中调整好入水姿势时池边的水平距离为m，问此次跳水会不会失误？通过计算说明理由．

某商场购进一批单价为16元的日用品，销售一段时间后，为了获得更多利润，商店决定提高销售价格．经试验发现，若按每件20元的价格销售时，每月能卖300件，若按每件25元的价格销售时，每月能卖210件，假定每月销售件数y(件)是价格x(元/件)的一次函数．

(1)试求y与x之间的函数关系式；

(2)在商品不积压，且不考虑其他因素的前提下，问销售价格定为多少时，才能使每月获得最大利润？每月的最大利润是多少？(总利润=总收入－总成本)

已知抛物线．

(1)证明：此抛物线与x轴总有两个不同的交点；

(2)a取何值时，两点间的距离最小？

设平方数是11个连续整数的平方和，求y的最小值．

已知：二次函数

(1)求证：二次函数的图像和x轴总有公共点．

(2)若此图像和x轴有两个公共点A、B且A(1，0)．求B点坐标．

某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米l000元．设矩形一边长为x米，面积为S平方米．

(1)求出S与x之间的函数关系式，并确定自变量x的取值范围；

(2)请你设计一个方案，使获得的设计费最多，并求出这个费用．