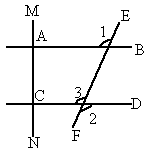
已知，如图，AB⊥MN，CD⊥MN，垂足分别为A、C，求证：∠1=∠2．

证明：∵AB⊥MN，CD⊥MN，

∴∠MAB=________=90°(　　　　　　)．

∴AB∥CD(　　　　　　)．

∴∠1=∠3(　　　　　　)．

又∵∠2=________(　　　　　　)，

∴∠1=∠2(　　　　　　)．

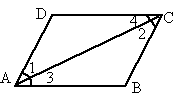
已知：如图，AD∥BC，∠BAD=∠BCD，

求证：AB∥CD．

证明：∵AD∥BC，

∴∠1=________(　　　　　　)．

又∵∠BAD=∠BCD，

∴∠BAD－∠1=∠BCD－∠2(　　　　　　)．

即∠3=∠4．

∴________∥________(　　　　　　)．

把下面证明过程补充完整．

已知：如图，MB∥DC，∠MAD=∠DCN，

求证：AD∥BN．

证明：∵MB∥DC(　　　　　　)．

∴∠B=________(　　　　　　)．

∵∠MAD=∠DCN(　　　　　　)．

∴∠B=________(　　　　　　)．

∴AD∥BN(　　　　　　)．

证明的过程是从________出发，经过________得出________．

在下列语句后面的横线上，填上所选择的字母．

(1)“同位角相等”是________；

(2)“两直线平行，则内错角相等”是________；

(3)“对顶角相等”是________；

(4)“两点之间线段最短”是________；

(5)“一组邻边相等的平行四边形是菱形”是________；

(6)“两条直线相交成直角，其中一条直线叫另一条直线的垂线”是________．

填入下面推理的依据，如图，已知∠A＋∠B=180°，

求证：∠C＋∠D=180°．

证明：∵∠A＋∠B=180°．

∴AD∥BC(　　　　　　)．

∴∠C＋∠D=180°(　　　　　　)．

推理的根据可以是________，也可以是________、________或________．

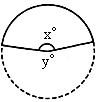
如图，扇子(阴影部分)的圆心角为x°，余下扇形的圆心角为y°，x与y的比通常按黄金比来设计，这样的扇子外形较美观．若黄金比为0.6，则x为________．

如下图，乐器上的一根弦AB=80cm，两个端点A、B固定在乐器板面上，支撑点C是靠近点B的黄金分割点(即AC、AB、BC满足关系式)，支撑点D是靠近点A的黄金分割点，则AC=________cm，DC=________cm．

(2006·宁夏)某中学将踢毽子作为趣味运动会的一个比赛项目，九年级(2)班同学进行了选拔测试，将所测试成绩进行整理，分成五组，并绘制成频数分布直方图如图．请结合直方图提供的信息，回答下列问题：

(1)该班共________名学生参加这次测试；

(2)60.5～70.5这一范围的频数为________，频率为________；

(3)这次测试成绩的中位数落在________范围内．