
科目: 来源: 题型:044
某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产76件,每件利润10元,每提高一个档次,每件利润增加2元,但一 天产量减少4件.
(1)
若生产第x档次的产品一天的总利润为y元(其中(2)
若生产第查看答案和解析>>
科目: 来源: 题型:044
阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a∶b).
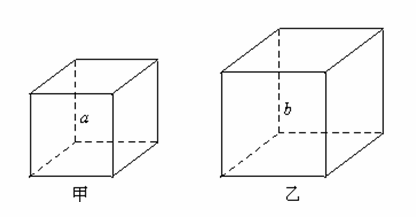
设S甲、S乙分别表示这两个正方体的表面积,则![]()
又设V甲、V乙分别表示这两个正方体的体积,则![]()
(1)
下列几何体中,一定属于相似体的是( )A
.两个球体 B.两个锥体 C.两个圆柱体 D.两个长方体(2)
请归纳出相似体的三条主要性质:①相似体的一切对应线段(或弧)长的比等于______;②相似体表面积的比等于______;③相似体体积比等于______.(3)
假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)查看答案和解析>>
科目: 来源: 题型:044
如图,抛物线![]() 交
交![]() 轴于A,B两点(点B在点A的左侧),交
轴于A,B两点(点B在点A的左侧),交![]() 轴于点C,其对称轴为
轴于点C,其对称轴为![]()
![]() 为坐标原点.
为坐标原点.
(1)求A,B,C三点的坐标;
(2)
求证:∠ACB是直角;(3)
抛物线上是否存在点P,使得∠APB为锐角?若存在,求出点P的横坐标的取值范围;若不存在,请说明理由.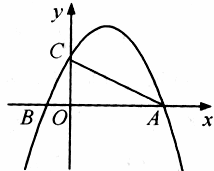
查看答案和解析>>
科目: 来源: 题型:044
如图,已知AB=AC,∠A=36o,AB的中垂线MN交AC于点D,交AB于点M.
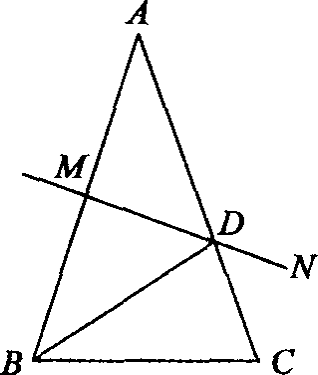
有下面4个结论:
①
射线BD是么ABC的平分线;②△BCD是等腰三角形;③△ABC∽△BCD
;④△AMD≌△BCD.(1)
判断其中正确的结论是哪几个?(2)
从你认为是正确的结论中选一个加以证明.查看答案和解析>>
科目: 来源: 题型:044
如图①,![]() 是圆
是圆![]() 的直径,
的直径,![]() 切圆
切圆![]() 于点
于点![]() ,
,![]() 与圆
与圆![]() 相交于点
相交于点![]() .
.
(1)
求证:(2)
如果将图①中的直线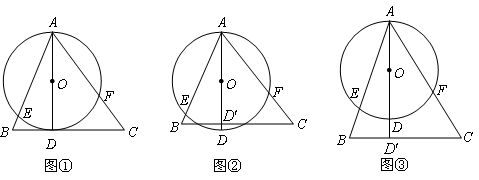
查看答案和解析>>
科目: 来源: 题型:044
如图1,线段![]() 过圆心
过圆心![]() ,交圆
,交圆![]() 于
于![]() 两点,
两点,![]() 切圆
切圆![]() 于点
于点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
(1)
写出图1中所有相等的角(直角除外),并给出证明;(2)
若图1中的切线(3)
在图2中,证明: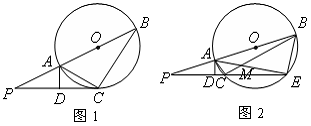
查看答案和解析>>
科目: 来源: 题型:044
如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() 重合),
重合),![]() ,
,![]() ,垂足分别为
,垂足分别为![]() .
.
(1)
求证:(2)
(3)
当
查看答案和解析>>
科目: 来源: 题型:044
如图,先把一矩形![]() 纸片对折,设折痕为
纸片对折,设折痕为![]() ,再把
,再把![]() 点叠在折痕线上,得到
点叠在折痕线上,得到![]() ,过
,过![]() 点折纸片使
点折纸片使![]() 点叠在直线
点叠在直线![]() 上,得折痕
上,得折痕![]() .
.
(1)
求作:(2)
你认为(3)
如果沿直线
查看答案和解析>>
科目: 来源: 题型:044
如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)
判断这两个三角形是否相似?并说明为什么?(2)
能否分别过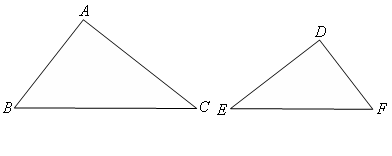
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com