假若用一根比地球赤道长1m的铁丝将地球赤道围起来，那么铁丝与赤道之间的间隙能有多大(把地球看成球形)?能放进一颗红枣吗?能放进一个拳头吗?

如图，已知BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4．

求证：AD∥BE．

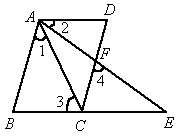
证明：∵AB∥CD(已知)，

∴∠4=∠________(两直线平行，同位角相等)．

∵∠3=∠4(已知)，

∴∠3=∠________(　　　)．

∵∠1=∠2(已知)，

∴∠1＋∠CAF=∠2＋∠CAF(　　)．

即∠________=∠________．

∴∠3：＝∠________(　　)，

∴AD∥BE(内错角相等，两直线平行)

已知：对于△ABC与△DEF，给出下列四个论断：

①∠A＝∠D；②AB=DE；③BC＝EF；④∠B=∠E．

请用以上其中三个论断作为条件，另一个作为结论，写出一个真命题，并给以证明．

命题“对于自然数n，代数式的值都是素数”是真命题还是假命题?请说明理由．

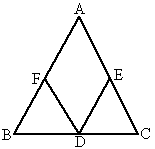
已知：如图，D，E，F分别是BC，CA，AB上的点，DE∥BA，DF∥CA．

求证：∠FDE=∠A．

证明：∵DE∥BA(已知)，

∴∠FDE=∠BFD(　　　　)．

∵DF∥CA(已知)，

∴∠BFD=________(　　　　)．

∵________=________(　　　　)．

如图，D是△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．

求证：CD=AF．

如图，已知AD⊥BC于D，EG⊥BC于G，∠1=∠E．

求证：AD为∠BAC的平分线．

如图，已知DE∥BC，EF∥AB，

求证：∠ADE=∠EFC．

当n=0，1，2，3，4，5时，代数式是质数吗？你能否得到结论，对所有的自然数n，的值都是质数．

以长为2的线段AB为边作正方形ABCD，取AB的中点P，连结PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上(如图所示)

(1)求AM、MD的长；

(2)你能说明点M是线段AD的黄金分割点吗?