
科目: 来源: 题型:044
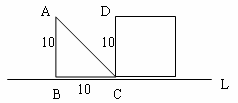
如图(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y![]() 。
。
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
查看答案和解析>>
科目: 来源: 题型:044
我市英山县某茶厂种植摯喝锱茢绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价![]() (元)与上市时间
(元)与上市时间![]() (天)的关系可以近似地用如图(1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价
(天)的关系可以近似地用如图(1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价![]() (元)与上市时间
(元)与上市时间![]() (天)的关系可以近似地用如图(2)的抛物线表示.
(天)的关系可以近似地用如图(2)的抛物线表示.

(2
)求出图(2)中表示的种植成本单价(3
)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(
说明:市场销售单价和种植成本单价的单位:元/500克.)查看答案和解析>>
科目: 来源: 题型:044
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示。
(1
)观察图象,当x为何值时,窗户透光面积最大?(3分)(2
)当窗户透光面积最大时,窗框的另一边长是多少?(2分)
查看答案和解析>>
科目: 来源: 题型:044
在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子。镜子的长与宽的比是2:1。已知镜面玻璃的价格是每平方米120元,边框的价格是每米20元,另外制作这面镜子还需加工费45元。设制作这面镜子的总费用是y元,镜子的宽度是x米。
(1
) 求y与x之间的关系式。(2
) 如果制作这面镜子共花了195元,求这面镜子的长和宽。查看答案和解析>>
科目: 来源: 题型:044
某机械租赁公司有同一型号的机械设备40套。经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出。在此基础上,当每套设备的月租金每提高10元时,这种设备就少租出一套,且没租出的一套设备每月需支出费用(维护费、管理费等)20元。设每套设备的月租金为x(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y(元)。
(1
)用含x的代数式表示未出租的设备数(套)以及所有未出租设备(套)的支出费(2
)求y与x之间的二次函数关系式;(3
)当月租金分别为300元和350元式,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由;(4
)请把(2)中所求出的二次函数配方成查看答案和解析>>
科目: 来源: 题型:044
农民张大伯为了致富奔小康,大力发展家庭养殖业。他准备用40m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形的羊圈。
(1) 请你求出张大伯矩形羊圈的面积;
(2) 请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由。

查看答案和解析>>
科目: 来源: 题型:044
右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
(1
)求抛物线的解析式.(2
)求两盏景观灯之间的水平距离.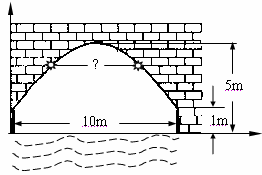

查看答案和解析>>
科目: 来源: 题型:044
有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图所示).
⑴请你直接写出O、A、M三点的坐标;
⑵一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)?

查看答案和解析>>
科目: 来源: 题型:044
路在山腹行是沪蓉西高速公路的显著特点之一,全线共有隧道37座,共计长达742421.2米。下图是正在修建的庙垭隧道的截面,截面是由一抛物线和一矩形构成,其行车道CD总宽度为8米,隧道为单行线2车道.
(1).建立恰当的平面直角坐标系,并求出隧道拱抛物线的解析式;
(2)在隧道拱的两侧距地面3米高处各安装一盏路灯,在(1)的平面直角坐标系中用坐标表示其中一盏路灯的位置;
(3) 为了保证行车安全,要求行驶车辆顶部
(设为平顶)与隧道拱在竖直方向上高度之差至少有0.5米。现有一辆汽车,装载货物后,其宽度为![]() 米,车载货物的顶部与路面的距离为2.5米,该车能否通过这个隧道?请说明理由。
米,车载货物的顶部与路面的距离为2.5米,该车能否通过这个隧道?请说明理由。

查看答案和解析>>
科目: 来源: 题型:044
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
(1)设矩形的一边为![]() (m),面积为
(m),面积为![]() (m2),求
(m2),求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2
)当
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com