
科目: 来源: 题型:044
利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
设每吨材料售价为x(元),该经销店的月利润为y(元).
(1
)当每吨售价是240元时,计算此时的月销售量;(2
)求出y与x的二次函数关系式(不要求写出x的取值范围);(3
)请把(2)中的二次函数配方成获得最大月利润,售价应定为每吨多少元;
(4)小静说:摰痹吕?笞畲笫保?孪?鄱钜沧畲螅當你认为对吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
如图所示,有一座抛物线形拱桥,桥下面在正常水位![]() 时,宽
时,宽![]() ,水位上升
,水位上升![]() 就达到警戒线
就达到警戒线![]() ,这时水面宽度为
,这时水面宽度为![]() .
.
(1
)在如图的坐标系中求抛物线的解析式;(2
)若洪水到来时,水位以每小时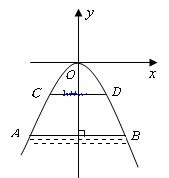
查看答案和解析>>
科目: 来源: 题型:044
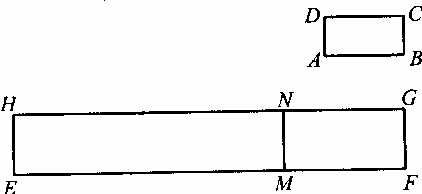
如图,在矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为边作矩形EMNH、矩形MFGN,使矩形MFGN∽矩形ABCD.令MN=![]() ,当
,当![]() 为何值时,矩形EMNH的面积S有最大值?最大值是多少?
为何值时,矩形EMNH的面积S有最大值?最大值是多少?
查看答案和解析>>
科目: 来源: 题型:044
王师傅有两块板材边角料,其中一块是边长为60![]() 的正方形板子;另一块是上底为30
的正方形板子;另一块是上底为30![]() ,下底为120
,下底为120![]() ,高为60
,高为60![]() 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点。
的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点。
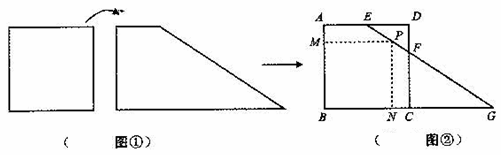
(1)求FC的长;
(2)利用图②求出矩形顶点B所对的顶点到BC边的距离![]() 为多少时,矩形的面积最大?最大面积时多少?
为多少时,矩形的面积最大?最大面积时多少?
(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
查看答案和解析>>
科目: 来源: 题型:044
某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
(1
)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积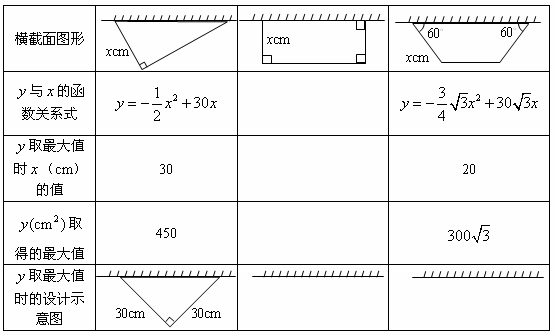
(2
)在研究性学习小组展示研究成果时,小华同学指出:图2中摰捉俏-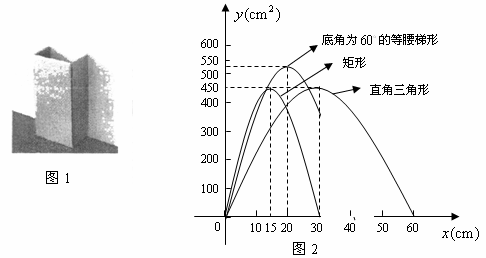
查看答案和解析>>
科目: 来源: 题型:044
利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1
)当每吨售价是240元时,计算此时的月销售量;(2
)求出y与x的函数关系式(不要求写出x的取值范围);(3
)该经销店要获得最大月利润,售价应定为每吨多少元?(4
)小静说:摰痹吕?笞畲笫保?孪?鄱钜沧畲螅當你认为对吗?请说明理由.查看答案和解析>>
科目: 来源: 题型:044
某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为y=-![]() x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y=![]() (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).
(1
)设P(x,y)是山坡线AB上任意一点,用y表示x,并求点B的坐标;(2
)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一起铺到山脚,为什么?
(3
)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道站的起点选择在山脚水平线上的点E处,OE=1600(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y=
查看答案和解析>>
科目: 来源: 题型:044
如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度。他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直地接触地面和门的内壁,并测得AC=1m。小强画出了如图的草图,请你帮他算一算门的高度OE(精确到0。1m)。
查看答案和解析>>
科目: 来源: 题型:044
某产品每件成本10元,在试销阶段每件产品的日销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
|
|
20 |
25 |
30 |
35 |
|
|
|
30 |
25 |
20 |
15 |
|
(1)在草稿纸上描点,观察点的分布,确定![]() 与
与![]() 的函数关系式.
的函数关系式.
(2
)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com