
科目: 来源: 题型:044
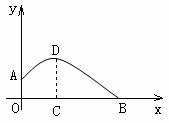
如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约![]() .铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
.铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
查看答案和解析>>
科目: 来源: 题型:044
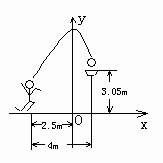
如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
查看答案和解析>>
科目: 来源: 题型:044
某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=![]() x2+5x+1000,Q=-
x2+5x+1000,Q=-![]() +45.
+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?
查看答案和解析>>
科目: 来源: 题型:044
某公司生产的A种产品,每件成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告.根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数,公司作了预测,知x与y之间的对应关系如下表:
|
x( 万元) |
0 |
1 |
2 |
… |
|
y |
1 |
1.5 |
1.8 |
… |
(1)
根据上表,求y关于x的函数关系式;(2)
如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元) 与广告费x(万元)的函数关系式;(3)
从上面的函数关系式中,你能得出什么结论?查看答案和解析>>
科目: 来源: 题型:044
画出函数![]() 的图象,根据图象回答问题:
的图象,根据图象回答问题:
(1)图象与x轴交点A的坐标_________,B点的坐标________,与y轴交点C 的坐标________,![]() =________.(A点在B点左边).
=________.(A点在B点左边).
(2)该函数的对称轴方程为_______,顶点P的坐标________,![]() =______.
=______.
(3)当______时,y≤0;当x_______时,y≥0.
(4)抛物线开口向________,函数y有最_____值;当x=_____时,y最值=______.
查看答案和解析>>
科目: 来源: 题型:044
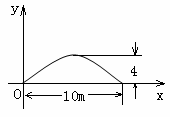
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)在对称轴右边1m处,桥洞离水面的高是多少?
查看答案和解析>>
科目: 来源: 题型:044
某商场经营一批进价为2元一件的小商品,在销售中发现此商品的日销售单价x(元)与日销售量y(件)间有如下关系:
|
x |
3 |
5 |
9 |
11 |
|
y |
18 |
14 |
6 |
2 |
(1)
在所给的如图所示的直角坐标系中:①
根据表中提供的数据描出实数对(x,y)的对应点;②猜测并确定日销售量y件与日销售单价x元间的函数关系式,并画出图象.
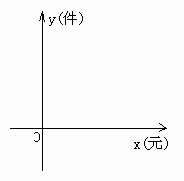
(2)
设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律:①
试求出日销售利润P元与日销售单价x元间的函数关系式, 并求出日销售单价为多少元时,才能获得最大日销售利润?试问日销售利润P是否存在最小值?若有, 试求出;若无,请说明理由.②
在给定的直角坐标系如图中,画出日销售利润P元与日销售单元x 之间的函数图象的简图,观察图象,写出x与P的取值范围.
查看答案和解析>>
科目: 来源: 题型:044
已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是![]() .
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
查看答案和解析>>
科目: 来源: 题型:044
已知如图所示,在平面直角坐标系xOy中,点A在第一象限,点A的纵坐标为3,∠AOx=60°.若有一点C,使∠AOC=30°,且线段![]() .
.
(1)求点C的坐标;
(2)若点B在Ox轴上,点C在第一象限,使△COB与△AOC相似.问是否存在一个二次函数,其图象经过A、B、C三点?若不存在,请说明理由;若存在,求出这个二次函数的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com