西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克．为了促销，该经营户决定降价销售．经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克．另外，每天的房租等固定成本共24元．该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？

如图，在矩形ABCD中，AB＝2AD，线段EF＝10．在EF上取一点M，分别以EM、MF为一边作矩形EMNH、矩形MFGN，使矩形MFGN∽矩形ABCD．令MN＝x，当x为何值时，矩形EMNH的面积S有最大值？最大值是多少？

某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示．这些农作物在第10天、第30天的需水量分别为2000千克、3000千克，在第40天后每天的需水量比前一天增加100千克．

(1)分别求出x≤40和x≥40时y与x之间的关系式；

(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉，那么应从第几天开始进行人工灌溉？

在平面直角坐标系中，直线l过点M(3，0)，且平行于y轴．

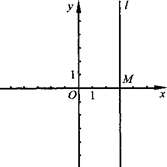
(1)如果△ABC三个顶点的坐标分别是A(－2，0)，B(－1，0)，C(－1，2)，△ABC关于y轴的对称图形是△A₁B₁C₁，△A₁B₁C₁关于直线l的对称图形是△A₂B₂C₁，写出△A₂B₂C₁的三个顶点的坐标；

(2)如果点P的坐标是(－a，0)，其中a＞0，点P关于y轴的对称点是P₁，点P₁关于直线l的对称点是P₂，求PP₂的长．

某校有A、B两个餐厅，甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐．

(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率；

(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率．

操作与探究：

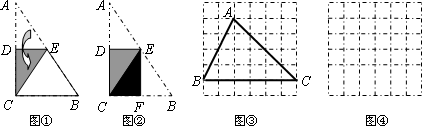
(1)图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；

(2)再将图①中的△CBE沿对称轴EF折叠(如图②)．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；

(3)请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；

(4)有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)．请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是，一定能折成组合矩形？

如图，⊙O是等腰三角形ABC的外接圆，AB＝AC，延长BC至点D，使CD＝AC，连接AD交⊙O与点E，连接BE、CE与AC交于点F．

(1)求证：△ABE≌△CDE；

(2)若AE＝6，DE＝9，求EF的长．

要在宽为28 m的海堤公路的路边安装路灯．路灯的灯臂长为3 m，且与灯柱成120°(如图所示)，路灯采用圆锥形灯罩，灯罩的轴线与灯臂垂直．当灯罩的轴线通过公路路面的中线时，照明效果最理想．问：应设计多高的灯柱，才能取得最理想的照明效果？(精确到0.01 m，)

为了营造出“城在林中、道在绿中、房在园中、人在景中”的城市新景象，市园林局计划在一定时间内完成100万亩绿化任务．现为配合东部城区大开发的需要，市政府在调研后将原定计划调整为：绿化面积在原计划的基础上增加20％，并且需提前1年完成．园林局经测算知，要完成新的计划，平均每年的绿化面积必须比原计划平均每年多10万亩．求原计划平均每年的绿化面积．

王强与李刚两位同学在学习“概率”时．做抛骰子(均匀正方体形状)实验，他们共抛了54次，出现向上点数的次数如下表：

(1)请计算出现向上点数为3的频率及出现向上点数为5的频率．

(2)王强说：“根据实验，一次试验中出现向上点数为5的概率最大．”

李刚说：“如果抛540次，那么出现向上点数为6的次数正好是100次．”

请判断王强和李刚说法的对错．

(3)如果王强与李刚各抛一枚骰子．求出现向上点数之和为3的倍数的概率．