小明与小亮玩游戏，他们将牌面数字分别是2，3，4的三张扑克牌兖分洗匀后，背面朝上放在桌面上．规定游戏规则如下：先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再从中随机抽出一张牌，将牌面数字作为个位上的数字．如果组成的两位数恰好是2的倍数．则小明胜；如果组成的两位数恰好是3的倍数．则小亮胜．

你认为这个游戏规则对双方公平吗？请用画数状图或列表的方法说明理由．

如图，在平面直角坐标系中，抛物线y＝ax²＋bx＋c(a≠0)的图象经过M(1，0)和N(3，0)两点，且与y轴交于D(0，3)，直线l是抛物线的对称轴．

(1)求该抛物线的解析式．

(2)若过点A(－1，0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6，求此直线的解析式．

(3)点P在抛物线的对称轴上，⊙P与直线AB和x轴都相切，求点P的坐标．

在喜迎建党九十周年之际，某校举办校园唱红歌比赛，选出10名同学担任评委，并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分)．

　　方案1：所有评委给分的平均分．

　　方案2：在所有评委中，去掉一个最高分和一个最低分，再计算剩余评委的平均分．

　　方案3：所有评委给分的中位数．

　　方案4：所有评委给分的众数．

为了探究上述方案的合理性，

先对某个同学的演唱成绩进行统计实验，下侧是这个同学的得分统计图：

(1)分别按上述四种方案计算这个同学演唱的最后得分．

(2)根据(1)中的结果，请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分？

已知梯形ABCD中，AD∥BC，AB＝AD(如图所示)，∠BAD的平分线AE交BC于点E，连接DE．

(1)在下图中，用尺规作∠BAD的平分线AE(保留作图痕迹不写作法)，并证明四边形ABED是菱形．

(2)若∠ABC＝60°，EC＝2BE．求证：ED⊥DC．

解不等式组把解集表示在数轴上，并求出不等式组的整数解．

已知菱形ABCD的边长为1．∠ADC＝60°，等边△AEF两边分别交边DC、CB于点E、F．

(1)特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；

(2)若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．

①猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；

②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断是否为定值．若是．请求出该定值；若不是．请说明理由．

已知抛物线y＝ax²＋bx＋c的对称轴为直线x＝2，且与x轴交于A、B两点．与y轴交于点C．其中AI(1，0)，C(0，－3)．

(1)求抛物线的解析式；

(2)若点P在抛物线上运动(点P异于点A)．

①如图l．当△PBC面积与△ABC面积相等时．求点P的坐标；

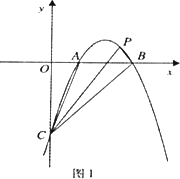
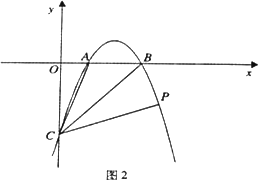
②如图2．当∠PCB＝∠BCA时，求直线CP的解析式．

某高科技公司根据市场需求，计划生产A、B两种型号的医疗器械，其部分信息如下：

　　信息一：A、B两种型号的医疔器械共生产80台．

　　信息二：该公司所筹生产医疗器械资金不少于1800万元，但不超过1810万元．且把所筹资金全部用于生产此两种医疗器械．

　　信息三：A、B两种医疗器械的生产成本和售价如下表：

根据上述信息．解答下列问题：

(1)该公司对此两种医疗器械有哪－几种生产方案？哪种生产方案能获得最大利润？

(2)根据市场调查，－每台A型医疗器械的售价将会提高a万元(a＞0)．

每台A型医疗器械的售价不会改变．该公司应该如何生产可以获得最大利润？

(注：利润＝售价－成本)

如图，将－矩形OABC放在直角坐际系中，O为坐标原点．点A在x轴正半轴上．点E是边AB上的－个动点(不与点A、N重合)，过点E的反比例函数的图象与边BC交于点F．

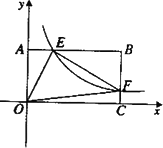
(1)若△OAE、△OCF的而积分别为S₁、S₂．且S₁＋S₂＝2，汆k的值：

(2)若OA＝2，OC＝4．问当点E运动到什么位置时．

四边形OAEF的面积最大．其最大值为多少？

如图，在Rt△ABC中，∠C＝90°，O、D分别为AB、BC上的点．经过A、D两点的⊙O分别交AB、AC于点E、F，且D为的中点．

(1)求证：BC与⊙O相切；

(2)当AD＝；∠CAD＝30°时．求的长，