如下图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

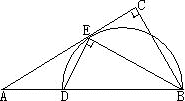
(1)求证：AC是△BDE的外接圆的切线；

(2)若，求EC的长．

高致病性禽流感是比SARS病毒传染速度更快的传染病．

(1)某养殖场有8万只鸡，假设有1只鸡得了禽流感，如果不采取任何防治措施，那么，到第二天将新增病鸡10只，到第三天又将新增病鸡100只，以后每天新增病鸡数依次类推，请问：到第四天，共有多少只鸡得了禽流感病？到第几天，该养殖场所有鸡都会被感染？

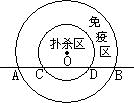
(2)为防止禽流感蔓延，政府规定：离疫点3千米范围内为扑杀区，所有禽类全部扑杀；离疫点3至5千米范围内为免疫区，所有的禽类强制免疫；同时，对扑杀区和免疫区内的村庄、道路实行全封闭管理．现有一条笔直的公路AB通过禽流感病区，如下图，O为疫点，在扑杀区内的公路CD长为4千米，问这条公路在该免疫区风有多少千米？

已知：如图△ABC内接于⊙O，OH⊥AC于H，过A点的切线与OC的延长线交于点D，∠B＝30°，．请求出：

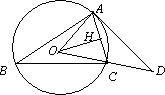
(1)∠AOC的度数；

(2)劣弧的长(结果保留π)；

(3)线段AD的长(结果保留根号)．

学完“几何的回顾”一章后，老师布置了一道思考题：

如图，点M，N分别在正三角形ABC的BC，CA边上，且BM＝CN，AM，BN交于点Q．求证：∠BQM＝60°．

(1)请你完成这道思考题；

(2)做完(1)后，同学们在老师的启发下进行了反思，提出了许多问题，如：

①若将题中“BM＝CN”与“∠BQM＝60°”的位置交换，得到的是否仍是真命题？

②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM＝60°？

③若将题中的条件“点M，N分别在正三角形ABC的BC，CA边上”改为“点M，N分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM＝60°？……

请你作出判断，在下列横线上填写“是”或“否”：①________；②________；③________．并对②，③的判断，选择一个给出证明．

定义[p，q]为一次函数y＝px＋q的特征数．

(1)若特征数是[2，k－2]的一次函数为正比例函数，求k的值；

(2)设点A，B分别为抛物线y＝(x＋m)(x－2)与x，y轴的交点，其中m＞0，且△OAB的面积为4，O为原点，求图象过A，B两点的一次函数的特征数．

地震发生后，一支专业搜救队驱车前往灾区救援．如图，汽车在一条南北走向的公路上向北行驶，当在A处时，车载GPS(全球卫星定位系统)显示村庄C在北偏西25°方向，汽车以35 km/h的速度前行2 h到达B处，GPS显示村庄C在北偏西50°方向．

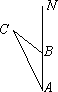
(1)求B处到村庄C的距离；

(2)求村庄C到该公路的距离．(结果精确到0.1 km)

(参考数据：sin26°≈0.4384，cos26°≈0.8988，sin52°≈0.7880，cos52°0.6157)

2008年5月1日，目前世界上最长的跨海大桥——杭州湾跨海大桥通车了．通车后，苏南A地到宁波港的路程比原来缩短了120千米．已知运输车速度不变时，行驶时间将从原来的3时20分缩短到2时．

(1)求A地经杭州湾跨海大桥到宁波港的路程；

(2)若货物运输费用包括运输成本和时间成本，已知某车货物从A地到宁波港的运输成本是每千米1.8元，时间成本是每时28元，那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元？

(3)A地准备开辟宁波方向的外运路线，即货物从A地经杭州湾跨海大桥到宁波港，再从宁波港运到B地．若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元，其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同，从宁波港到B地的海上运费对一批不超过10车的货物计费方式是：一车800元，当货物每增加1车时，每车的海上运费就减少20元，问这批货物有几车？

如图，□ABCD中，AB＝4，点D的坐标是(0，8)，以点C为顶点的抛物线y＝ax²＋bx＋c经过x轴上的点A、B．

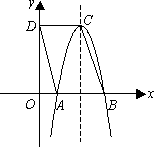
(1)求点A、B、C的坐标．

(2)若抛物线向上平移后恰好经过点D，求平移后抛物线的解析式．

1月底，某公司还有11000千克椪柑库存，这些椪柑的销售期最多还有60天，60天后库存的椪柑不能再销售，需要当垃圾处理，处理费为0.05元/吨．经测算，椪柑的销售价格定为2元/千克时，平均每天可售出100千克，销售价格降低，销售量可增加，每降低0.1元/千克，每天可多售出50千克．

(1)如果按2元/千克的价格销售，能否在60天内售完这些椪柑？按此价格销售，获得的总毛利润是多少元(总毛利润=销售总收入－库存处理费)？

(2)设椪柑销售价格定为x(0＜x≤2)元/千克时，平均每天能售出y千克，求y关于x的函数解析式；如果要在2月份售完这些椪柑(2月份按28天计算)，那么销售价格最高可定为多少元/千克(精确到0.1元/千克)？

如图，在平面直角坐标系中，Rt△OAB的直角边OA在x轴的正半轴上，点B在第象限，将△OAB绕点O按逆时针方向旋转至△O，使点B的对应点落在y轴的正半轴上，已知OB＝2，∠BOA＝30°

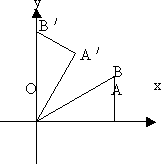
(1)求点B和点的坐标；

(2)求经过点B和点的直线所对应的一次函数解析式，并判断点A是否在直线B上．