如图，在直角梯形纸片ABCD中，AB∥DC，∠A＝90°，CD＞AD，将纸片沿过点D的直线折叠，使点A落在边CD上的点E处，折痕为DF．连接EF并展开纸片．

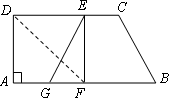
(1)求证：四边形ADEF是正方形；

(2)取线段AF的中点G，连接EG，如果BG＝CD，试说明四边形GBCE是等腰梯形．

如图，在等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12．动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．

(1)梯形ABCD的面积等于________；

(2)当PQ∥AB时，P点离开D点的时间等于________秒；

(3)当P、Q、C三点构成直角三角形时，P点离开D点多少时间？

如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点．训练时要求A、B两船始终关于O点对称．以O为原点．建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线上运动，湖面风平浪静，双帆远影优美．训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置(假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示)．

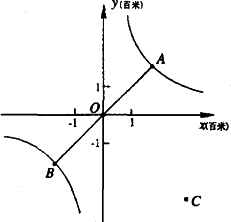
(1)发现C船时，A、B、C三船所在位置的坐标分别为A(________，________)、B(________，________)和C(________，________)；

(2)发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3∶4，问教练船是否最先赶到？请说明理由．

在“5·12大地震”灾民安置工作中，某企业接到一批生产甲种板材24000 m²和乙种板材12000 m²的任务．

(1)已知该企业安排140人生产这两种板材，每人每天能生产甲种板材30 m²或乙种板材20 m²．问：应分别安排多少人生产甲种板材和乙种板材，才能确保他们用相同的时间完成各自的生产任务？

(2)某灾民安置点计划用该企业生产的这批板材搭建A，B两种型号的板房共400间，在搭建过程中，按实际需要调运这两种板材．已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示：

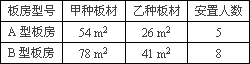
问：这400间板房最多能安置多少灾民？

如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．

(1)求证：四边形AECD是菱形；

(2)若点E是AB的中点，试判断△ABC的形状，并说明理由．

如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．

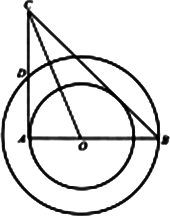
(1)试判断BC所在直线与小圆的位置关系，并说明理由；

(2)试判断线段AC、AD、BC之间的数量关系，并说明理由；

(3)若AB＝8 cm，BC＝10 cm，求大圆与小圆围成的圆环的面积．(结果保留π)

某校师生积极为汶川地震灾区捐款，在得知灾区急需帐篷后，立即到当地的一家帐篷厂采购，帐篷有两种规格：可供3人居住的小帐篷，价格每顶160元；可供10人居住的大帐篷，价格每顶400元．学校花去捐款96000元，正好可供2300人临时居住．

(1)求该校采购了多少顶3人小帐篷，多少顶10人大帐篷；

(2)学校现计划租用甲、乙两种型号的卡车共20辆将这批帐篷紧急运往灾区，已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷，乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷．如何安排甲、乙两种卡车可一次性将这批帐篷运往灾区？有哪几种方案？

如图，在△ABD和ACE中，AB＝AD，AC＝AE，∠BAD＝∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．

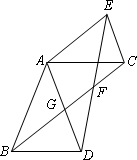
(1)试判断线段BC、DE的数量关系，并说明理由；

(2)如果∠ABC＝∠CBD，那么线段FD是线段FG和FB的比例中项吗？为什么？

已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断

①OA＝OC　②AB＝CD　③∠BAD＝∠DCB　④AD∥BC

请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：

①构造一个真命题，画图并给出证明；

②构造一个假命题，举反例加以说明．

为缓解油价上涨给出租车待业带来的成本压力，某巿自2007年11月17日起，调整出租车运价，调整方案见下列表格及图像(其中a，b，c为常数)

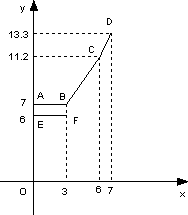
设行驶路程xkm时，调价前的运价y₁(元)，调价后的运价为y₂(元)如图，折线ABCD表示y₂与x之间的函数关系式，线段EF表示当0≤x≤3时，y₁与x的函数关系式，根据图表信息，完成下列各题：

①填空：a＝________，b＝________，c＝________．

②写出当x＞3时，y₁与x的关系，并在上图中画出该函数的图象．

③函数y₁与y₂的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由．