如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE＝EB，连接PD，O为AC中点．

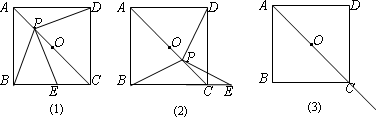
(1)如图(1)，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；

(2)如图(2)，当点P在线段OC上时，(1)中的猜想还成立吗？请说明理由；

(3)如图(3)，当点PAC的延长线上时，请你在图3中画出相应的图形(尺规作图，保留作图痕迹，不写作法)，并判断(1)中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．

随着人们生活水平的提高，轿车已进入平常百姓家，我市家庭轿车的拥有量也逐年增加．某汽车经销商计划用不低于228万元且不高于240万元的资金订购30辆甲、乙两种新款轿车．两种轿车的进价和售价如下表：

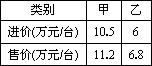
(1)请你帮助经销商算一算共有哪几种进货方案？

(2)如果按表中售价全部卖出，哪种进货方案获利最多？并求出最大利润．

(注：其他费用不计，利润＝售价－进价)

如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A(－2，0)、B(0，1)、C(d，2)．

(1)求d的值；

(2)将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点、正好落在某反比例函数图像上．请求出这个反比例函数和此时的直线的解析式；

(3)在(2)的条件下，直线BC交y轴于点G．问是否存在x轴上的点M和反比例函数图像上的点P，使得四边形PGM是平行四边形．如果存在，请求出点M和点P的坐标；如果不存在，请说明理由．

如下图，已知△ABC中，AB＝10 cm，AC＝8 cm，BC＝6 cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2 cm/s．连接PQ，设运动的时间为t(单位：s)(0≤t≤4)．解答下列问题：

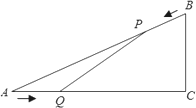
(1)当t为何值时，PQ∥BC．

(2)设△AQP面积为S(单位：cm²)，当t为何值时，S取得最大值，并求出最大值．

(3)是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．

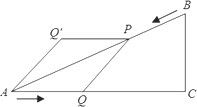
(4)如下图，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．

如图，点O为坐标原点，直线绕着点A(0，2)旋转，与经过点C(0，1)的二次函数交于不同的两点P、Q．

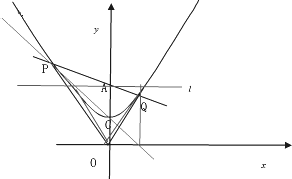
(1)求h的值；

(2)通过操作、观察算出△POQ面积的最小值；

(3)过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中四边形AOBQ是否为梯形，若是，请说明理由；若不是，请指明其形状．

如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为(－3，0)、(0，4)，抛物线y＝x²＋bx＋c经过点B，且顶点在直线x＝上．

(1)求抛物线对应的函数关系式；

(2)若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；

(3)在(2)的条件下，连接BD，已知对称轴上存在一点P使得△PBD的周长最小，求出P点的坐标；

(4)在(2)、(3)的条件下，若点M是线段OB上的一个动点(点M与点O、B不重合)，过点M作∥BD交x轴于点N，连接PM、PN，设OM的长为t，△PMN的面积为S，求S和t的函数关系式，并写出自变量t的取值范围，S是否存在最大值？若存在，求出最大值和此时M点的坐标；若不存在，说明理由．

若x₁、x₂是关于一元二次方程ax²＋bx＋c(a≠0)的两个根，则方程的两个根x₁、x₂和系数a、b、c有如下关系：x₁＋x₂＝－，x₁·x₂＝．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax²＋bx＋c(a≠0)的图象与x轴的两个交点为A(x₁，0)，B(x₂，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：

AB＝|x₁－x₂|＝＝＝＝．

参考以上定理和结论，解答下列问题：

设二次函数y＝ax²＋bx＋c(a＞0)的图象与x轴的两个交点A(x₁，0)、B(x₂，0)，抛物线的顶点为C，显然△ABC为等腰三角形．

(1)当△ABC为直角三角形时，求b²－4ac的值；

(2)当△ABC为等边三角形时，求b²－4ac的值．

如图，抛物线y＝ax²－x－2(a≠0)的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为(4，0)．

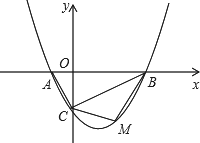
(1)求抛物线的解析式；

(2)试探究△ABC的外接圆的圆心位置，并求出圆心坐标；

(3)若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．

如图，在⊙O上位于直径AB的异侧有定点C和动点P，AC＝AB，点P在半圆弧AB上运动(不与A、B两点重合)，过点C作直线PB的垂线CD交PB于D点．

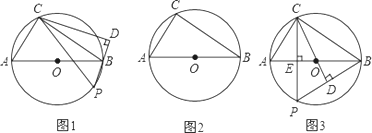
(1)如图1，求证：△PCD∽△ABC；

(2)当点P运动到什么位置时，△PCD≌△ABC？请在图2中画出△PCD并说明理由；

(3)如图3，当点P运动到CP⊥AB时，求∠BCD的度数．

如图，抛物线与x轴交于C、A两点，与y轴交于点B，OB＝4点O关于直线AB的对称点为D，E为线段AB的中点．

(1)分别求出点A、点B的坐标

(2)求直线AB的解析式

(3)若反比例函数的图像过点D，求k值．

(4)两动点P、Q同时从点A出发，分别沿AB、AO方向向B、O移动，点P每秒移动1个单位，点Q每秒移动个单位，设△POQ的面积为S，移动时间为t，问：S是否存在最大值？若存在，求出这个最大值，并求出此时的t值，若不存在，请说明理由．