
科目: 来源:2008年广东省肇庆市初中毕业升学统一考试、数学试卷 题型:044
如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙O于点E.
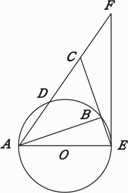
(1)求证AE=CE;
(2)EF与⊙O相切于点E,交AC的延长线于点F,若CD=CF=2 cm,求⊙O的直径;
(3)若![]() (n>0),求sin∠CAB.
(n>0),求sin∠CAB.
查看答案和解析>>
科目: 来源:2008年广东省深圳市初中毕业升学统一考试、数学试卷 题型:044
“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目: 来源:2008年广东省梅州市初中毕业升学统一考试、数学试卷 题型:044
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
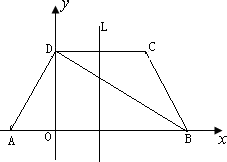
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使△PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
查看答案和解析>>
科目: 来源:2008年广东省中山市初中毕业升学统一考试、数学试卷 题型:044
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图1,AC=________,BD=________;四边形ABCD是________梯形.
(2)请写出图1中所有的相似三角形(不含全等三角形).
(3)如图2,若以AB所在直线为x轴,过点A垂直于AB的直线为y轴建立如图2的平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
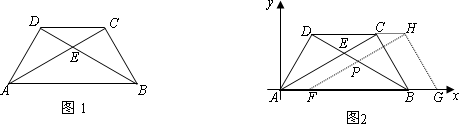
查看答案和解析>>
科目: 来源:2008年广东省东莞市初中毕业升学统一考试、数学试卷 题型:044
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图1,AC=________,BD=________;四边形ABCD是________梯形.
(2)请写出图1中所有的相似三角形(不含全等三角形).
(3)如图2,若以AB所在直线为x轴,过点A垂直于AB的直线为y轴建立如图2的平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
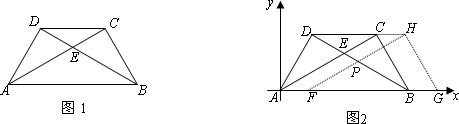
查看答案和解析>>
科目: 来源:2008年山东省青岛市初中毕业升学统一考试、数学试卷 题型:044
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
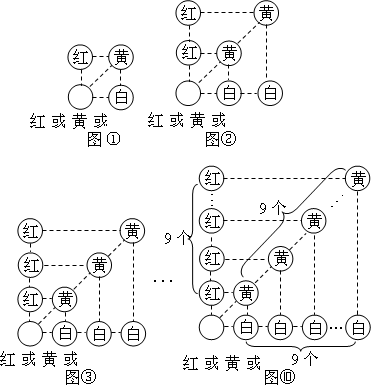
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:1+3=4(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是:1+3×2=7(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是:1+3×3=10(如图③):
……
(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:1+3×(10-1)=28(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是________;
(3)若要确保摸出的小球至少有n个同色(n<20),则最少需摸出小球的个数是________.
模型拓展二:在不透明口袋中装有m种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________.
(2)若要确保摸出的小球至少有n个同色(n<20),则最少需摸出小球的个数是________.
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
查看答案和解析>>
科目: 来源:2008年山东省聊城市初中毕业升学统一考试、数学试卷 题型:044
如图,把一张长10 cm,宽8 cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
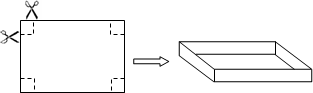
(1)要使长方体盒子的底面积为48 cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
查看答案和解析>>
科目: 来源:2008年山东省聊城市初中毕业升学统一考试、数学试卷 题型:044
小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图1),它的侧面边缘上有两条圆弧(如图2),其中顶部圆弧AB的圆心Q1在竖直边缘AD上,另一条圆弧BC的圆心O2在水平边缘DC的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计,π取3.1416).
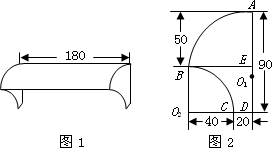
(1)计算出弧AB所对的圆心角的度数(精确到0.01度)及弧AB的长度(精确到0.1 cm);
(2)计算出遮雨罩一个侧面的面积(精确到1 cm2);
(3)制做这个遮雨罩大约需要多少平方米的玻璃钢材料(精确到0.1平方米)?
查看答案和解析>>
科目: 来源:2008年山东省潍坊市初中毕业升学统一考试、数学试卷 题型:044
如图,圆B切y轴于原点O,过定点A(-2![]() ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=![]() ,抛物线C经过A、P两点.
,抛物线C经过A、P两点.
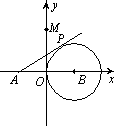
(1)求圆B的半径.
(2)若抛物线C经过点B,求其解析式.
(3)设抛物线C交y轴于点M,若三角形APM为直角三角形,求点M的坐标.
查看答案和解析>>
科目: 来源:2008年山东省潍坊市初中毕业升学统一考试、数学试卷 题型:044
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.
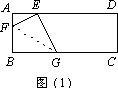
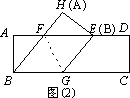
(1)当折痕的另一端F在AB边上时,如图(1).求△EFG的面积.
(2)当折痕的另一端F在AD边上时,如图(2).证明四边形BGEF为菱形,并求出折痕GF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com