
科目: 来源:2008年江西省初中毕业升学统一考试、数学试卷 题型:044
如图1,正方形ABCD和正三角形EFG的边长都为1,点E,F分别在线段AB,AD上滑动,设点G到CD的距离为x,到BC的距离为y,记∠HEF为α(当点E,F分别与B,A重合时,记α=0°).

(1)当α=0°时(如图2所示),求x,y的值(结果保留根号);
(2)当α为何值时,点G落在对角线AC上?请说出你的理由,并求出此时x,y的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):

(4)若将“点E,F分别在线段AB,AD上滑动”改为“点E,F分别在正方形ABCD边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点G运动所形成的大致图形.
(参考数据:![]() .)
.)
查看答案和解析>>
科目: 来源:2008年江西省初中毕业升学统一考试、数学试卷 题型:044
已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).
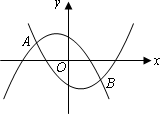
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当a=![]() 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线l,l1,l2都垂直于x轴,l1,l2分别经过A,B两点,l在直线l1,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值.
查看答案和解析>>
科目: 来源:2008年江苏省镇江市初中毕业升学统一考试、数学试卷 题型:044
如图,在直角坐标系xOy中,点P为函数y=![]() x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R.
x2在第一象限内的图象上的任一点,点A的坐标为(0,1),直线l过B(0,-1)且与x轴平行,过P作y轴的平行线分别交x轴,l于C,Q,连结AQ交x轴于H,直线PH交y轴于R.

(1)求证:H点为线段AQ的中点;
(2)求证:①四边形APQR为平行四边形;
②平行四边形APQR为菱形;
(3)除P点外,直线PH与抛物线y=![]() x2有无其它公共点?并说明理由.
x2有无其它公共点?并说明理由.
查看答案和解析>>
科目: 来源:2008年江苏省镇江市初中毕业升学统一考试、数学试卷 题型:044
阅读以下材料:
对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:
![]() ;min{-1,2,3}=-1;min{-1,2,a}=
;min{-1,2,3}=-1;min{-1,2,a}=![]()
解决下列问题:
(1)填空:min{sin30°,cos45°,tan30°}=________;
如果min{2,2x+2,4-2x}=2,则x的取值范围为________≤x≤________.
(2)①如果M(2,x+1,2x)=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么________(填a,b,c的大小关系)”.证明你发现的结论;
③运用②的结论,填空:
若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=________.
(3)在同一直角坐标系中作出函数y=x+1,y=(x-1)2,y=2-x的图象(不需列表描点).通过观察图象,填空:min{x+1,(x-1)2,2-x}的最大值为________.
查看答案和解析>>
科目: 来源:2008年江苏省连云港市初中毕业升学统一考试、数学试卷 题型:044
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
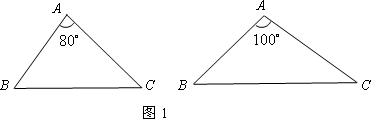
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
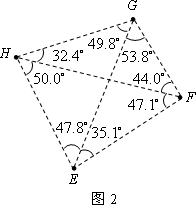
(3)某地有四个村庄E,F,G,H(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
查看答案和解析>>
科目: 来源:2008年江苏省连云港市初中毕业升学统一考试、数学试卷 题型:044
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的△AOB,△COD处,直角边OB,OD在x轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
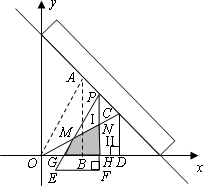
(1)求直线AC所对应的函数关系式;
(2)当点P是线段AC(端点除外)上的动点时,试探究:
①点M到x轴的距离h与线段BH的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积S是否存在最大值?若存在,求出这个最大值及S取最大值时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2008年江苏省连云港市初中毕业升学统一考试、数学试卷 题型:044
“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共9千顶,现某地震灾区急需帐篷14千顶,该集团决定在一周内赶制出这批帐篷.为此,全体职工加班加点,总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于两市通住A,B两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:

请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
查看答案和解析>>
科目: 来源:2008年江苏省苏州市初中毕业升学统一考试、数学试卷 题型:044
课堂上,老师将图①中△AOB绕O点逆时针旋转,在旋转中发现图形的形状和大小不变,但位置发生了变化当△AOB旋转90°时,得到△A1OB1.已知A(4,2)、B(3,0).
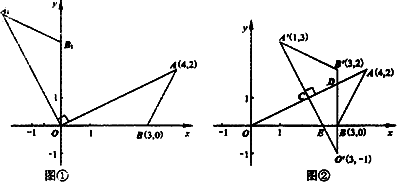
(1)△A1OB1的面积是________;A1点的坐标为(________,________;B1点的坐标为(________,________);
(2)课后,小玲和小惠对该问题继续进行探究,将图②中△AOB绕AO的中点C(2,1)逆时针旋转90°得到△![]() ,设
,设![]() 交OA于D,
交OA于D,![]()
![]() 交x轴于E.此时
交x轴于E.此时![]() 、
、![]() 和
和![]() 的坐标分别为(1,3)、(3,-1)和(3,2),且
的坐标分别为(1,3)、(3,-1)和(3,2),且![]() 经过B点.在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CFBD的面积;
经过B点.在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CFBD的面积;
(3)在(2)的条件一下,△AOB外接圆的半径等于________.
查看答案和解析>>
科目: 来源:2008年江苏省无锡市初中毕业升学统一考试、数学试卷 题型:044
一种电讯信号转发装置的发射直径为31 km.现要求:在一边长为30 km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30 km的正方形城区示意图,供解题时选用)
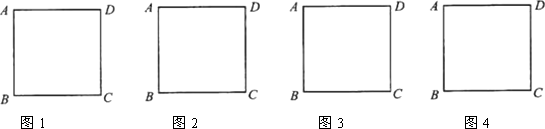
查看答案和解析>>
科目: 来源:2008年江苏省无锡市初中毕业升学统一考试、数学试卷 题型:044
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
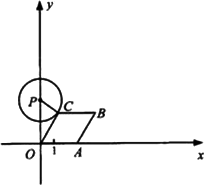
(1)点C的坐标(用含t的代数式表示);
(2)当点A在运动过程中,所有使⊙P与菱形OABC的边所在直线相切的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com