在平面直角坐标系内有两点A(－2，0)，，CB所在直线为y＝2x＋b，

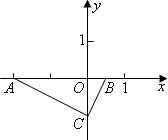
(1)求b与C的坐标

(2)连结AC，求证：△AOC∽△COB

(3)求过A，B，C三点且对称轴平行于y轴的抛物线解析式

(4)在抛物线上是否存在一点P(不与C重合)，使得S_△ABP＝S_△ABC，若存在，请求出P点坐标，若不存在，请说明理由．

已知抛物线C₁：y＝－x²＋2mx＋n(m，n为常数，且m≠0，n＞0)的顶点为A，与y轴交于点C；抛物线C₂与抛物线C₁关于y轴对称，其顶点为B，连接AC，BC，AB．

注：抛物线y＝ax²＋bx＋c(a≠0)的顶点坐标为．

(1)请在横线上直接写出抛物线C₂的解析式：________；

(2)当m＝1时，判定△ABC的形状，并说明理由；

(3)抛物线C₁上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．

某旅游胜地欲开发一座景观山．从山的侧面进行堪测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位：百米)．已知AB所在抛物线的解析式为y＝－x²＋8，BC所在抛物线的解析式为y＝(x－8)²，且已知B(m，4)．

(1)设P(x，y)是山坡线AB上任意一点，用y表示x，并求点B的坐标；

(2)从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20厘米，长度因坡度的大小而定，但不得小于20厘米，每级台阶的两端点在坡面上(见图)．

①分别求出前三级台阶的长度(精确到厘米)；

②这种台阶不能一直铺到山脚，为什么？

(3)在山坡上的700米高度(点D)处恰好有一小块平地，可以用来建造索道站．索道的起点选择在山脚水平线上的点E处，OE＝1600(米)．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y＝(x－16)²．试求索道的最大悬空高度．

如图，已知抛物线C₁与坐标轴的交点依次是A(－4，0)，B(－2，0)，E(0，8)．

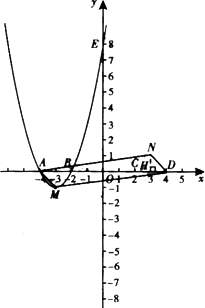
(1)求抛物线C₁关于原点对称的抛物线C₂的解析式；

(2)设抛物线C₁的顶点为M，抛物线C₂与x轴分别交于C，D两点(点C在点D的左侧)，顶点为N，四边形MDNA的面积为S．若点A，点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M，点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A与点D重合为止．求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值范围；

(3)当t为何值时，四边形MDNA的面积S有最大值，并求出此最大值；

(4)在运动过程中，四边形MDNA能否形成矩形？若能，求出此时t的值；若不能，请说明理由．

如图，点E在正方形ABCD的边CD上运动，AC与BE交于点F．

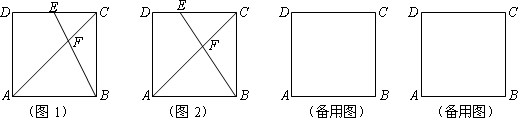
(1)如图1，当点E运动到DC的中点时，求△ABF与四边形ADEF的面积之比；

(2)如图2，当点E运动到CE∶ED＝2∶1时，求△ABF与四边形ADEF的面积之比；

(3)当点E运动到CE∶ED＝3∶1时，写出△ABF与四边形ADEF的面积之比；当点E运动到CE∶ED＝n∶1(n是正整数)时，猜想△ABF与四边形ADEF的面积之比(只写结果，不要求写出计算过程)；

(4)请你利用上述图形，提出一个类似的问题．

如图，直线分别与y轴，x轴相交于点A，点B，且AB＝5．一个圆心在坐标原点，半径为1的圆，以0.8个单位/秒的速度向y轴正方向运动．设此动圆圆心离开坐标原点的时间为t(t≥0)(秒)．

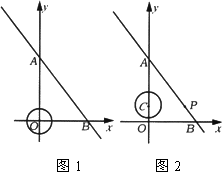
(1)求直线AB的解析式；

(2)如图1，t为何值时，动圆与直线AB相切？

(3)如图2，若在圆开始运动的同时，一动点P从B点出发，沿BA方向以1个单位/秒的速度运动，设t秒时点P到动圆圆心C的距离为s，求s与t的关系式；

(4)在(3)中，动点P自刚接触圆面起，经多长时间后离开了圆面？

如图，在某气象站M附近海面有一台风，据监测，当前台风中心位于气象站M的东偏南方向100千米的海面P处，并以20千米/小时的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为20千米，并以10千米/小时的速度不断增大，已知，问：

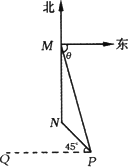
(1)台风中心几小时移动到气象站M正南N处，此时气象站M是否受台风侵袭？

(2)几小时后该气象站开始受台风的侵袭？

已知抛物线y＝ax²＋bx＋c过点，其顶点E的横坐标为2，此抛物线与x轴分别交于B(x₁，0)，C(x₂，0)两点(x₁＜x₂)，且．

(1)求此抛物线的解析式及顶点E的坐标；

(2)若D是y轴上一点，且△CDE为等腰三角形，求点D的坐标．

把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC＝∠DEF＝90°，∠C＝∠F＝45°，AB＝DE＝4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q．

(1)如图1，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ．此时，AP·CQ＝_________．

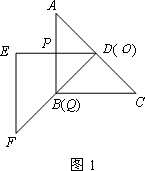
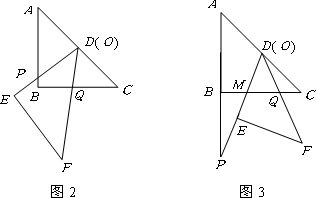
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AP·CQ的值是否改变？说明你的理由．

(3)在(2)的条件下，设CQ＝x，两块三角板重叠面积为y，求y与x的函数关系式．(图2，图3供解题用)

如图，在直角坐标系中，以点为半径的圆与x轴相交于点B，C，与y轴相交于点D，E．

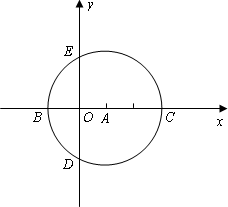
(1)若抛物线经过C，D两点，求抛物线的解析式，并判断点B是否在该抛物线上．

(2)在(1)中的抛物线的对称轴上求一点P，使得△PBD的周长最小．

(3)设Q为(1)中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M，使得四边形BCQM是平行四边形．若存在，求出点M的坐标；若不存在，说明理由．