已知抛物线y＝ax²＋bx＋c的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C(0，3)，过点C作x轴的平行线与抛物线交于点D，抛物线的顶点为M，直线y＝x＋5经过D、M两点．

(1)求此抛物线的解析式；

(2)连接AM、AC、BC，试比较∠MAB和∠ACB的大小，并说明你的理由．

已知：如图，△ABC是边长3 cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1 cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t(s)，解答下列问题：

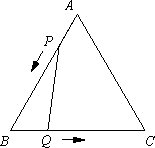
(1)当t为何值时，△PBQ是直角三角形？

(2)设四边形APQC的面积为y(cm²)，求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出相应的t值；不存在，说明理由；

(3)设PQ的长为x(cm)，试确定y与x之间的关系式．

提出问题：如图，在四边形ABCD中，P是AD边上任意一点，△PBC与△ABC和△DBC的面积之间有什么关系？

探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：

(1)当AP＝AD时(如图)：

∵AP＝AD，△ABP和△ABD的高相等，

∴S_△ABP＝S_△ABD．

∵PD＝AD－AP＝AD，△CDP和△CDA的高相等，

∴S_△CDP＝S_△CDA．

∴S_△PBC＝S_{四边形ABCD}－S_△ABP－S_△CDP

＝S_{四边形ABCD}－S_△ABD－S_△CDA

＝S_{四边形ABCD}－(S_{四边形ABCD}－S_△DBC)－(S_{四边形ABCD}－S_△ABC)

＝S_△DBC＋S_△ABC．

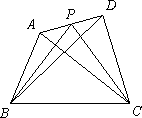
(2)当时，探求S_△PBC与S_△ABC和S_△DBC之间的关系，写出求解过程；

(3)当时，S_△PBC与S_△ABC和S_△DBC之间的关系式为：________；

(4)一般地，当(n表示正整数)时，探求S_△PBC与S_△ABC和S_△DBC之间的关系，写出求解过程；

问题解决：当时，S_△PBC与S_△ABC和S_△DBC之间的关系式为：________．

如图，已知正方形ABCD的边长与Rt△PQR的直角边PQ的长均为4 cm，QR＝8 cm，AB与QR在同一条直线l上．开始时点Q与点B重合，让△PQR以1 cm/s速度在直线l上运动，直至点R与点A重合为止，ts时△PQR与正方形ABCD重叠部分的面积记为S cm²．

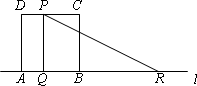
(1)当t＝3 s时，求S的值；

(2)求S与t之间的函数关系式，并写出自变量t的取值范围；

(3)写出t为何值时，重叠部分的面积S有最大值，最大值是多少？

矩形OABC在平面直角坐标系中位置如图所示，A、C两点的坐标分别为A(6，0)，C(0，－3)，直线与BC边相交于D点．

(1)求点D的坐标；

(2)若抛物线经过点A，试确定此抛物线的表达式；

(3)设(2)中的抛物线的对称轴与直线OD交于点M，点P为对称轴上一动点，以P、O、M为顶点的三角形与△OCD相似，求符合条件的点P的坐标．

如图，在梯形ABCD中，AD∥BC，AD＝2，BC＝4，点M是AD的中点，△MBC是等边三角形．

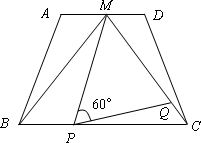
(1)求证：梯形ABCD是等腰梯形；

(2)动点P、Q分别在线段BC和MC上运动，且∠MPQ＝60°保持不变．设PC＝x，MQ＝y，求y与x的函数关系式；

(3)在(2)中：①当动点P、Q运动到何处时，以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；

②当y取最小值时，判断△PQC的形状，并说明理由．

如图，在平面直角坐标系中，O为坐标原点，边长为5的正三角形OAB的OA边在x轴的正半轴上．点C、D同时从点O出发，点C以1单位长/秒的速度向点A运动，点D为2个单位长/秒的速度沿折线OBA运动．设运动时间为t秒，0＜t＜5．

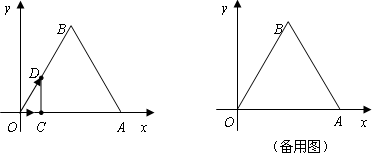
(1)当时，证明DC⊥OA；

(2)若△OCD的面积为S，求S与t的函数关系式；

(3)以点C为中心，将CD所在的直线顺时针旋转60°交AB边于点E，若以O、C、E、D为顶点的四边形是梯形，求点E的坐标．

如图，边长为1的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形，EF与GH交于点P．

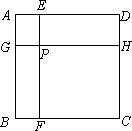
(1)若AG＝AE，证明：AF＝AH；

(2)若∠FAH＝45°，证明：AG＋AE＝FH；

(3)若Rt△GBF的周长为1，求矩形EPHD的面积．

已知二次函数y＝x²－x＋c．

(1)若点A(－1，a)、B(2，2n－1)在二次函数y＝x²－x＋c的图象上，求此二次函数的最小值；

(2)若点D(x₁，y₁)、E(x₂，y₂)、P(m，n)(m＞n)在二次函数y＝x²－x＋c的图象上，且D、E两点关于坐标原点成中心对称，连接OP．当时，试判断直线DE与抛物线的交点个数，并说明理由．

我们知道，当一条直线与一个圆有两个公共点时，称这条直线与这个圆相交．类似地，我们定义：当一条直线与一个正方形有两个公共点时，称这条直线与这个正方形相交．

如图，在平面直角坐标系中，正方形OABC的顶点为O(0，0)、A(1，0)、B(1，1)、C(0，1)．

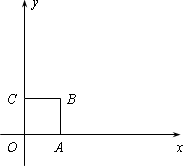
(1)判断直线与正方形OABC是否相交，并说明理由；

(2)设d是点O到直线的距离，若直线与正方形OABC相交，求d的取值范围．