
科目: 来源:广东省汕头市濠江区2010届九年级中考模拟考试数学试题 题型:044
已知:如图,直线y=-![]() x+4
x+4![]() 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=![]() x相交于点P.
x相交于点P.

(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:①S与t之间的函数关系式.
②当t为何值时,S最大,并求S的最大值.
查看答案和解析>>
科目: 来源:广东省汕头市潮阳区2010届九年级中考模拟数学试题 题型:044
如图,在梯形ABCD中,AD∥BC,AB=AD=DC=4,∠A=120°.动点P、E、M分别从B、A、D三点同时出发,其中点P沿BA向终点A运动,点E沿AD向终点D运动,点M沿DC向终点C运动,且它们的速度都为每秒2个单位.连结PE、PM、EM,设动点P、E、M运动时间为t(单位:秒),△PEM的面积为S.
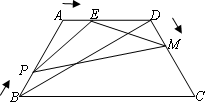
(1)判断△PAE与△EDM是否全等,说明理由;
(2)连结BD,求证:△EPM∽△ABD;
(3)求S与t的函数关系式,并求出△PEM的面积的最小值.
查看答案和解析>>
科目: 来源:广东省汕头市潮阳区2010届九年级中考模拟数学试题 题型:044
某单位为了优化办公条件,已经两次更新部分电脑和空调:第一次购买1台品牌电脑和2台品牌空调,共花费9500元;第二次购买2台品牌电脑和1台品牌空调,共花费11500元.适逢最近国务院出台家电“以旧换新”政策,该单位决定采用“以旧换新”的方式进一步更新电脑和空调(前后三次品牌电脑和品牌空调的型号和价格都相同).“以旧换新”政策中规定:消费者交售旧家电后凭以旧换新凭证购买新家电时直接申领补贴,国家给予以旧换新的消费者10%的补贴,将补贴资金抵减新家电销售价格后支付,其中,电脑最高补贴400元,空调最高补贴350元.
(1)购买一台这款品牌空调和一台这款品牌空调所需的资金分别是多少元?
(2)按家电“以旧换新”政策,购买了一台这款品牌电脑和一台这款品牌空调,消费者可分
别获得多少元的政府补贴?
(3)该单位预算用不超过30000元资金,连同交售十台旧家电所得的资金总额1500元,购买这款品牌电脑和这款品牌空调共10台(其中至少有1台电脑).请你通过计算求出有几种购买方案,并写出所有的方案.
查看答案和解析>>
科目: 来源:北京市2006年高级中等学校招生统一考试(课标B卷)数学试卷 题型:044
已知抛物线y=ax2+bx+c与y轴交于点A(0,3),与x轴分别交于B(1,0),C(5,0)两点.
(1)求此抛物线的解析式;
(2)若点D为线段OA的一个三等分点,求直线DC的解析式;
(3)若一个动点P自OA的中点M出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A.求使点P运动的总路径最短的点E,点F的坐标,并求出这个最短总路径的长.
查看答案和解析>>
科目: 来源:江苏省徐州市2007年初中毕业、升学考试数学试题 题型:044
如图,直线l1∶y=-x+1与两直线l2∶y=2x、l3∶y=x分别交于M、N两点.设点P为x轴上的一点,过点P的直线l∶y=-x+b与直线l2、l3分别交于A、C两点,以线段AC为对角线作正方形ABCD.
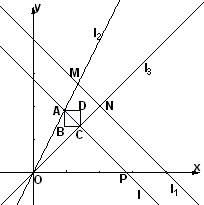
(1)写出正方形ABCD个顶点的坐标(用b表示);
(2)当点P从原点O出发,沿着x轴的正方向运动时,设正方形ABCD与△OMN重叠部分的面积为S,求S与b之间的函数关系式,并写出相应自变量的取值范围.
查看答案和解析>>
科目: 来源:江苏省徐州市2007年初中毕业、升学考试数学试题 题型:044
如图,△ABC中,点D在AC上,点E在BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转得到△C![]()
![]() (使∠BC
(使∠BC![]() <180°),连接A
<180°),连接A![]() 、B
、B![]() 设直线B
设直线B![]() 与AC、A
与AC、A![]() 分别交于点O、E.
分别交于点O、E.
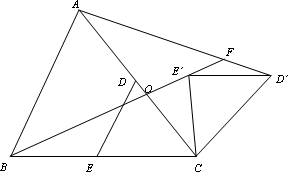
(1)若△ABC为等边三角形,则![]() 的值为________,∠AFB的度数为________,(2)若△ABC满足∠ACB=60°,AC=
的值为________,∠AFB的度数为________,(2)若△ABC满足∠ACB=60°,AC=![]() ,BC=
,BC=![]() ,
,
①求![]() 的值和∠AFB的度数
的值和∠AFB的度数
②若E为BC的中点,求△OBC面积的最大值.
查看答案和解析>>
科目: 来源:吉林省长春市2007年初中毕业生学业考试数学试题 题型:044
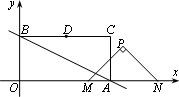
如图,在平面直角坐标系中,直线![]() (b>0)分别交x轴、y轴于A、B两点,以OA、OB为边作矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.
(b>0)分别交x轴、y轴于A、B两点,以OA、OB为边作矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.
(1)求点P的坐标;
(2)当b值由小到大变化时,求S与b的函数关系式;
(3)若在直线![]() (b>0)上存在点Q,使∠OQM等于90°,请直接写出b的取值范围;
(b>0)上存在点Q,使∠OQM等于90°,请直接写出b的取值范围;
(4)在b值的变化过程中,若△PCD为等腰三角形,请直接写出所有符合条件的b值.
查看答案和解析>>
科目: 来源:吉林省2007年初中毕业生学业考试数学试题 题型:044
如图①,在边长为![]() cm的正方形ABCD中,E、F是对角线AC上的两个动点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC交Rt△ACD的直角边于H;过F作FG垂直AC交Rt△ACD的直角边于G,连接HG、EB.设HE、EF、FG、GH围成的图形面积为S1,AE、EB、BA围成的图形面积为S2(这里规定:线段的面积为0).E到达C,F到达A停止.若E的运动时间为xs,解答下列问题:
cm的正方形ABCD中,E、F是对角线AC上的两个动点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC交Rt△ACD的直角边于H;过F作FG垂直AC交Rt△ACD的直角边于G,连接HG、EB.设HE、EF、FG、GH围成的图形面积为S1,AE、EB、BA围成的图形面积为S2(这里规定:线段的面积为0).E到达C,F到达A停止.若E的运动时间为xs,解答下列问题:

(1)当0<x<8时,直接写出以E、F、G、H为顶点的四边形是什么四边形,并求出x为何值时,S1=S2;
(2)①若y是S1与S2的和,求y与x之间的函数关系式;(图②为备用图)
②求y的最大值.
查看答案和解析>>
科目: 来源:吉林省2007年初中毕业生学业考试数学试题 题型:044
今年4月18日,我国铁路第六次大提速,在甲、乙两城市之间开通了动车组高速列车.已知每隔1 h有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(单位在:km)与运行时间t(单位:h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(单位:km)与运行时间t(单位:h)的函数图象.请根据图中信息,解答下列问题:
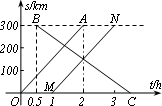
(1)点B的横坐标0.5的意义是普通快车发车时间比第一列动车组列车发车时间________h,点B的纵坐标300的意义是________;
(2)请你在原图中直接画出第二列动车组列车离开甲城的路程s(单位:km)与时间t(单位:h)的函数图象;
(3)若普通快车的速度为100 km/h,
①求BC的解析式,并写出自变量t的取值范围;
②求第二列动车组列车出发后多长时间与普通列车相遇;
③直接写出这列普通列车在行驶途中与迎面而来的相邻两列动车组列车相遇的间隔时间.
查看答案和解析>>
科目: 来源:2007年广东省茂名市初中毕业生学业考试与高中阶段学校招生考试数学试题 题型:044
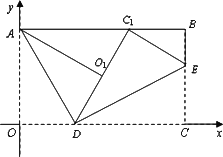
如图,已知平面直角坐标系xoy中,有一矩形纸片OABC,O为坐标原点,AB∥x轴,B(3,![]() ),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30°.折叠后,点O落在点O1,点C落在点C1,并且DO1与DC1在同一直线上.
),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30°.折叠后,点O落在点O1,点C落在点C1,并且DO1与DC1在同一直线上.
(1)求折痕AD所在直线的解析式;
(2)求经过三点O,C1,C的抛物线的解析式;
(3)若⊙P的半径为R,圆心P在(2)的抛物线上运动,⊙P与两坐标轴都相切时,求⊙P半径R的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com