抛物线y＝ax²＋bx＋c(a＜0)交x轴于点A(－1，0)、B(3，0)，交y轴于点C，顶点为D，以BD为直径的⊙M恰好过点C．

(1)求顶点D的坐标(用a的代数式表示)；

(2)求抛物线的解析式；

(3)抛物线上是否存在点P使△PBD为直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

如图，已知△ABC中，∠＝90°，∠B＝60°，AC＝4，等边△DEF的一边在直角边AC上移动，当点E与点c重合时，点D恰好落在AB边上，

(1)求等边△DEF的边长；

(2)请你探索，在移动过程中，线段CE与图中哪条线段始终保持相等，并说明理由；

(3)若设线段CE为x，在移动过程中，等边△BEF与Rt△ABC两图形重叠部分的面积为y．请你写出y与x的函数关系式，并写出自变量x的取值范围．

如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S₁、S₂、S₃表示，则不难证明S₁＝S₂＋S₃．

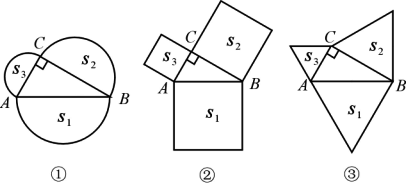
(1)如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S₁、S₂、S₃表示，那么S₁、S₂、S₃之间有什么关系？(不必证明)

(2)如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S₁、S₂、S₃表示，请你确定S₁、S₂、S₃之间的关系并加以证明；

(3)若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S₁、S₂、S₃表示，为使S₁、S₂、S₃之间仍具有与(2)相同的关系，所作三角形应满足什么条件？证明你的结论；

(4)类比(1)、(2)、(3)的结论，请你总结出一个更具一般意义的结论．

函数y＝－的图象分别交x轴，y轴于A，C两点，

(1)求出A、C两点的坐标．

(2)在x轴上找出点B，使ΔACB∽ΔAOC，若抛物线经过A、B、C三点，求出抛物线的解析式．

(3)在(2)的条件下，设动点P、Q分别从A、B两点同时出发，以相同的速度沿AC、BA向C、A运动，连结PQ，设AP＝m，是否存在m值，使以A、P、Q为顶点的三角形与ΔABC相似，若存在，求出所有的m值；若不存在，请说明理由．

初三(几何)课本中有这样一道习题，若⊙O₁与⊙O₂外切于点A，BC是两圆的一条外公切线，B、C为切点，则AB⊥AC

(1)若⊙O₁和⊙O₂外离，BC为两圆的外公切线，B，C为切点，连心线O₁O₂分别交⊙O₁，⊙O₂于M，N，设BM与CN的延长线交于A，试问AB与AC是否垂直？证明你的结论．

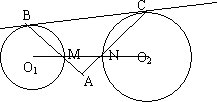
(2)若⊙O₁与⊙O₂相交，AB与AC垂直吗？

已知抛物线y＝x²＋(2n－1)x＋n²－1(n为常数)．

(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；

(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．

①当BC＝1时，求矩形ABCD的周长；

②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由．

如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2，E为BC的中点，以OE为直径的⊙O’交x轴于D点，过点D作DF⊥AE于F

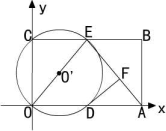
(1)求OA、OC的长；

(2)求证：DF为⊙O’的切线

(3)小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O’外”．你同意他的看法吗？请充分说明理由

在如下图所示的直角坐标系中，已知直角梯形OACD的边长OA＝8、OD＝、CD＝2、AC＝，点B的横坐标为5，直线a∥b，且直线a的解析式为y＝x．现使直角梯形OACD沿着x轴以每秒1个单位的速度向右平移．设在平移中t秒时直角梯形夹在直线a，b之间的部分面积为S

(1)当0＜t＜13时，求S与t的函数解析式；

(2)在0＜t＜13的范围内，S是否有最大值？如果有最大值，请求出最大值，否则请说明理由．

某校研究性学习小组在研究有关二次函数及其图象性质的问题时，发现了两个重要的结论：一是发现抛物线y＝ax²＋2x＋3(a≠0)，当实数a变化时，它的顶点都在某条直线上；二是发现当实数a变化时，若把抛物线y＝ax²＋2x＋3的顶点的横坐标减少，纵坐标增加，得到A点的坐标；若把顶点的横坐标增加，纵坐标增加，得到B点的坐标，则A、B两点一定仍在抛物线y＝ax²＋2x＋3上．

(1)请你协助探求实数a变化时，抛物线y＝ax²＋2x＋3的顶点所在直线的解析式；

(2)问题(1)中的直线上有一个点不是该抛物线的顶点，你能找出它来吗？并说明理由；

(3)在他们第二个发现的启发下，运用“一般——特殊——一般”的思想，你还能发现什么？你能用数学语言将你的猜想表述出来吗？你的猜想成立吗？若能成立，请说明理由．