如图，已知抛物线的顶点为A(2，1)，且经过原点O，与x轴的另一个交点为B．

(1)求抛物线的解析式；

(2)在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；

(3)连结OA、AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标；若不存在，所们理由．

在平面直角坐标系中给定以下五个点．

(1)请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；

(2)求该抛物线的顶点坐标和对称轴，并画出草图；

(3)已知点F(－1，)在抛物线的对称轴上，直线过点且垂直于对称轴．验证：以E(1，0)为圆心，EF为半径的圆与直线相切．请你进一步验证，以抛物线上的点为圆心DF为半径的圆也与直线相切．由此你能猜想到怎样的结论．

如图(1)，两半径为r的等圆⊙O₁和⊙O₂相交于M，N两点，且⊙O₂过点O₁．过M点作直线AB垂直于MN，分别交⊙O₁和⊙O₂于A，B两点，连结NA，NB．

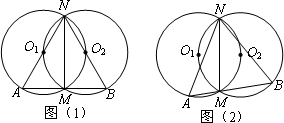
(1)猜想点O₂与⊙O₁有什么位置关系，并给出证明；

(2)猜想△NAB的形状，并给出证明；

(3)如图(2)，若过M的点所在的直线AB不垂直于MN，且点A，B在点M的两侧，那么(2)中的结论是否成立，若成立请给出证明．

两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED，按如图一所示的位置放置，点O与E重合．

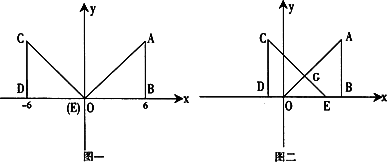
(1)Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长度的速度向右运动，当点E运动到与点B重合时停止，设运动x秒后，Rt△AOB和Rt△CED的重叠部分面积为y，求y与x之间的函数关系式；

(2)当Rt△CED以(1)中的速度和方向运动，运动时间x＝2秒时，Rt△CED运动到如图二所示的位置，若抛物线过点A，G，求抛物线的解析式；

(3)现有一动点P在(2)中的抛物线上运动，试问点P在运动过程中是否存在点P到x轴或y轴的距离为2的情况，若存在，请求出点P的坐标；若不存在，请说明理由．

如图，AB是⊙O的直径，点C在⊙O上，∠BOC＝108°，过点C作直线CD分别交直线AB和⊙O于点D、E，连接OE，DE＝AB，OD＝2．

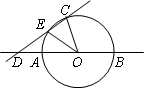
(1)求∠BDC的度数；

(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比(或者底边长与腰长的比)等于．

①写出图中所有的黄金三角形，选一个说明理由；

②求弦CE的长；

③在直线AB或CD上是否存在点P(点C、D除外)，使△POE是黄金三角形？若存在，画出点P，简要说明画出点P的方法(不要求证明)；若不存在，说明理由．

已知抛物线y＝x²＋(2n－1)x＋n²－1(n为常数)．

(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；

(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．

①当BC＝1时，求矩形ABCD的周长；

②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由．

如图，一次函数y＝x＋m图象过点A(1，0)，交y轴于点B，C为y轴负半轴上一点，且BC＝2OB，过A、C两点的抛物线交直线AB于点D，且CD∥x轴．

(1)求这条抛物线的解析式；

(2)观察图象，写出使一次函数值小于二次函数值时x的取值范围；

(3)在题中的抛物线上是否存在一点M，使得∠ADM为直角？若存在，求出点M的坐标；若不存在，请说明理由．

如图1，在矩形ABCD中，AB＝20 cm，BC＝4 cm．点P从A开始沿折线A－B－C－D以4 cm/s的速度移动，点Q从C开始沿CD边以1 cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动．设运动时间为t(s)．

(1)点P与点Q，谁先到达D点？此时运动的时间是多少秒？

(2)当t＝4秒时，试说明四边APQD是怎样特殊的四边形？

(3)如图2，如果⊙P和⊙Q的半径都是2 cm．

①求当t为何值时，⊙P和⊙Q外切？

②⊙P和⊙Q从开始运动到停止运动的过程中，求⊙P和⊙Q外离时，t的取值范围(不要求说明理由，只须写出答案即可)________

如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙交x轴于D点，过点D作DF⊥AE于点F．

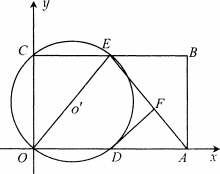
(1)求OA、OC的长；

(2)求证：DF为⊙的切线；

(3)小明在解答本题时，发现△AOE是等腰三角形．

他与同学小刚一起研究：“直线BC上除点E以外还存在其它点P，使△AOP也是等腰三角形吗？”结果发现还有其它点．小明说：点P一定在⊙外．你同意他的看法吗？请充分说明理由．并把所有满足条件的点的坐标表示出来．

如图1，正△ABC和正△FDE，F与B重合，AB与FD在一条直线上．

(1)若将△FDE绕点B旋转一定角度(如图2)，试说明CD＝AE；

(2)已知AB＝6，DE＝，把图(1)中的△FDE绕点B逆时针方向旋转90°(如图3)，试判断四边形EBDC的形状，并说明你的理由；

(3)若把图(1)中的正△FDE沿BA方向平移(如图4)，连结AE、BE，已知正△ABC和正△FDE的边长分别是5 cm和 cm，问在平移过程中，△ABE是否会成为等腰三角形？若能，直接写出FB的值；若不能，说明理由．