如图，点O是坐标原点，点A(n，0)是x轴上一动点(n＜0)．以AO为一边作矩形AOBC，使OB＝2OA，点C在第二象限．将矩形AOBC绕点A逆时针旋转90°得矩形AGDE．过点A得直线y＝kx＋m(k≠0)交y轴于点F，FB＝FA．抛物线y＝ax²＋bx＋c过点E、F、G且和直线AF交于点H，过点H作x轴的垂线，垂足为点M．

(1)求k的值；

(2)点A位置改变使，△AMH的面积和矩形AOBC的面积比是否改变？说明你的理由．

已知：AC是⊙O的直径，点A、B、C、O在⊙O上OA＝2．建立如图所示的直角坐标系．∠ACO＝∠ACB＝60°．

(1)求点B关于x轴对称的点D的坐标；

(2)求经过三点A、B、O的二次函数的解析式；

(3)该抛物线上是否存在在点P，使四边形PABO为梯形？若存在，请求出P点的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为－1，直线l：y＝－x－与坐标轴分别交于A、C两点，点B的坐标为(4，1)，⊙B与x轴相切于点M．

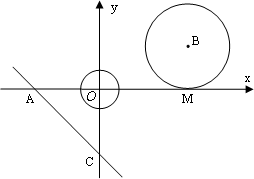
(1)求点A的坐标及∠CAO的度数；

(2)⊙B以每秒1各单位长度的速度沿x轴负方向平移，同时，直线l绕点A顺时针匀速旋转．当⊙B第一次与⊙O相切时，直线l也恰好与⊙B第一次相切．问：直线AC绕点A每秒旋转多少度？

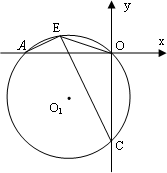
(3)如下图，过A、O、C三点作⊙O₁，点E为劣弧上一点，连接EC、EA、EO，当点E在劣弧上运动时(不与A、O两点重合)，的值是否发生变化？如果不变，求其值；如果变化，说明理由．

已知：将一副三角板(Rt△ABC和Rt△DEF)如图①摆放，点E、A、D、B在一条直线上，且D是AB的中点．将Rt△DEF绕点D顺时针方向旋转角α(0°＜α＜90°)，在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H．

(1)当α＝30°时(如图②)，求证：AG＝DH；

(2)当α＝60°时(如图③)，(1)中的结论是否成立？请写出你的结论，并说明理由；

(3)当0°＜α＜90°时，(1)中的结论是否成立？请写出你的结论，并根据图④说明理由．

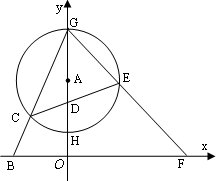
已知平面直角坐标系中，B(－3，0)，A为y轴正半轴上一动点，半径为的⊙A交y轴于点G、H(点G在点H的上方)，连接BG交⊙A于点C．

(1)如图，当⊙A与x轴相切时，求直线BG的解析式；

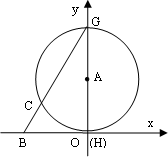
(2)如图，若CG＝2BC，求OA的长；

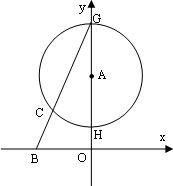
(3)如图，D为半径AH上一点，且AD＝1，过点D作⊙A的弦CE，连结GE并延长交x轴于点F，当⊙A与x轴相离时，给出下列结论：①的值不变；②OG·OF的值不变．其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．

已知：二次函数y＝x²－(m＋1)x＋m的图象交x轴于A(x₁，0)、B(x₂，0)两点，交y轴正半轴于点C，且．

(1)求此二次函数的解析式；

(2)是否存在过点D(0，)的直线与抛物线交于点M、N，与x轴交于点E，使得点M、N关于点E对称？若存在，求直线MN的解析式；若不存在，请说明理由．

已知抛物线y＝ax²＋bx＋2与x轴相交于点A(x₁，0)，B(x₂，0)(x₁＜x₂)，且x₁，x₂是方程x²－2x－3＝0的两个实数根，点C为抛物线与y轴的交点．

(1)求a，b的值；

(2)分别求出直线AC和BC的解析式；

(3)若动直线y＝m(0＜m＜2)与线段AC，BC分别相交于D，E两点，则在x轴上是否存在点P，使得△DEP为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．