
科目: 来源:广东省实验中学2010届初中毕业班一模考试数学试题 题型:059
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出m的值及四边形ABEF的面积;若不存在,请说明理由.
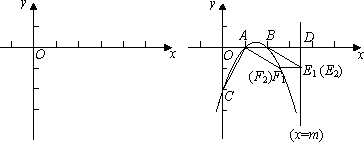
查看答案和解析>>
科目: 来源:广东省实验中学2010届初中毕业班一模考试数学试题 题型:059
(1)如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图,在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.

查看答案和解析>>
科目: 来源:广东省汕头市潮阳区2010届九年级中考模拟数学试题 题型:059
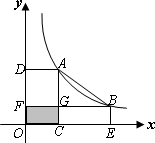
如图,点A、B是双曲线y=![]() (k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
(k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
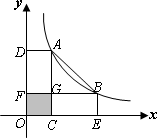
(1)求双曲线的解析式;
(2)在双曲线上移动点A和点B,上述作图不变,得到矩形OCGF(阴影部分),点A、B在运动过程中始终保持S阴影=1不变(如图),则△AGB的面积是否会改变?说明理由.
查看答案和解析>>
科目: 来源:北京市2006年高级中等学校招生统一考试(课标B卷)数学试卷 题型:059
我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
查看答案和解析>>
科目: 来源:2006年辽宁省锦州市中考数学试题 题型:059
如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
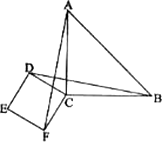
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源:2006年江苏省常州市初中毕业、升学统一考试数学试题 题型:059
如下图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
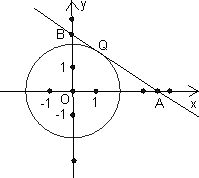
(1)点P在运动时,线段AB的长度页在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q、O、A、P为顶点的四边形时平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2006年湖南省郴州市课改实验区初中毕业学业考试试卷数学 题型:059
已知抛物线y=ax2+bx+c经过P(![]() ,3),E
,3),E![]() 及原点O(0,0).
及原点O(0,0).
(1)求抛物线的解析式.
(2)过P点作平行于x轴的直线PC交y轴于C点,在抛物线对称轴右侧且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC(如下图).是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,请说明理由.

(3)如果符合(2)中的Q点在x轴的上方,连结OQ,矩形OABC内的四个三角形△OPC,△PQB,△OQP,△OQA之间存在怎样的关系?为什么?
查看答案和解析>>
科目: 来源:2006年湖南省郴州市课改实验区初中毕业学业考试试卷数学 题型:059
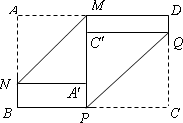
如图1,矩形纸片ABCD的边长分别为a,b(a<b).将纸片任意翻折(如图2),折痕为PQ.(P在BC上),使顶点C落在四边形APCD内一点![]() ,
,![]() 的延长线交直线AD于M,再将纸片的另一部分翻折,使A落在直线PM上一点
的延长线交直线AD于M,再将纸片的另一部分翻折,使A落在直线PM上一点![]() ,且
,且![]() 所在直线与PM所在直线重合(如图3)折痕为MN.
所在直线与PM所在直线重合(如图3)折痕为MN.

(1)猜想两折痕PQ,MN之间的位置关系,并加以证明.
(2)若∠QPC的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕PQ,MN间的距离有何变化?请说明理由.
(3)若∠QPC的角度在每次翻折的过程中都为45°(如下图),每次翻折后,非重叠部分的四边形![]() ,及四边形
,及四边形![]() 的周长与a,b有何关系,为什么?
的周长与a,b有何关系,为什么?
查看答案和解析>>
科目: 来源:2006年湖南省常德市初中毕业生学业考试数学试卷 题型:059
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如下图,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP·CQ=_________.

(2)将三角板DEF由上图所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图1,图2供解题用)

查看答案和解析>>
科目: 来源:2006年湖南省常德市初中毕业生学业考试数学试卷 题型:059
如下图,在直角坐标系中,以点A(![]() ,0)为圆心,以
,0)为圆心,以![]() 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
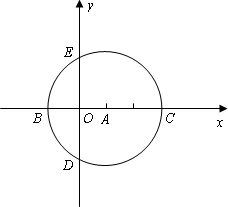
(1)若抛物线y=![]() x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上.
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上.
(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小.
(3)设Q为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形.若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com