
科目: 来源:湖北省咸宁市2010年中考数学试卷 题型:059
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
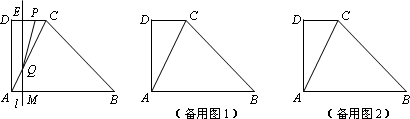
(1)当t=0.5时,求线段QM的长;
(2)当0<t<2时,如果以
C、P、Q为顶点的三角形为直角三角形,求t的值;(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源:湖北省咸宁市2010年中考数学试卷 题型:059
问题背景
(1)如图,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
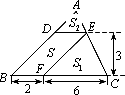
四边形DBFE的面积S=________,
△EFC的面积S1=________,
△ADE的面积S2=________.
探究发现
(2)在(1)中,若BF=a,FC=b,DE与BC间的距离为h.请证明S2=4S1S2.
拓展迁移
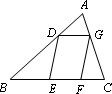
(3)如图,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.
查看答案和解析>>
科目: 来源:湖北省荆门市2010年初中毕业生学业考试数学试卷 题型:059
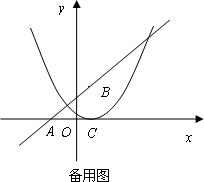
已知:如图一次函数y=![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)

(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
查看答案和解析>>
科目: 来源:河南省2010届初中学业水平暨高级中等学校招生考试数学试题 题型:059
(1)操作发现
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在举行ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源:广东省深圳市2010年初中毕业生学业考试数学试卷 题型:059
如图,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=-![]() x-
x-![]() 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.
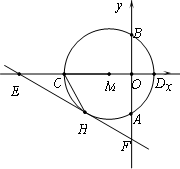
(1)请直接写出OE、⊙M的半径r、CH的长;
(2)如图,弦HQ交x轴于点P,且DP:PH=3∶2,求cos∠QHC的值;
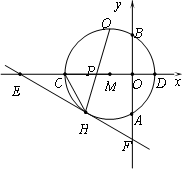
(3)如图,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一![]() 个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.

查看答案和解析>>
科目: 来源:福建省南平市2010年中考数学试题 题型:059
如图,已知点B(1,3)、C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.

(1)填空:A点坐标为(________,________),D点坐标为(________,________);
(2)若抛物线y=![]() x2+bx+c经过C、D两点,求抛物线的解析式;
x2+bx+c经过C、D两点,求抛物线的解析式;
(3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.
(提示:抛物线y=ax2+bx+c(a≠0)的对称轴是x=-![]() ,顶点坐标是(-
,顶点坐标是(-![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源:2010年云南省玉溪市中考数学试题 题型:059
如图,在平面直角坐标系中,点A的坐标为(1,![]() ),△AOB的面积是
),△AOB的面积是![]() .
.
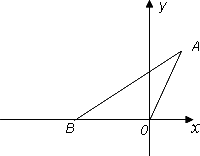
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2∶3?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2010年四川省达州市高中阶段招生考试数学试题 题型:059
如图,对称轴为x=3的抛物线y=ax2+2x与x轴相交于点B、O
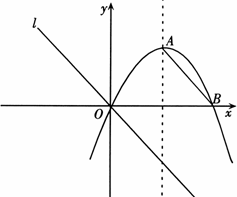
(1)求抛物线的解析式,并求出顶点A的坐标;
(2)连结AB,把AB所在的直线平移,使它经过原点O,得到直线l.点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;
(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边.若存在,直接写出点Q的坐标;若不存在,说明理由
查看答案和解析>>
科目: 来源:2010年陕西省初中毕业升学考试数学试题 题型:059
问题探究
(1)请你在图中做一条直线,使它将矩形ABCD分成面积相等的两部分;

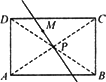
(2)如图点M是矩形ABCD内一点,请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
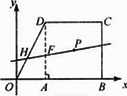
(3)如图,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,CD=4开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处.为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且是这条路所在的直线l将直角梯形OBCD分成面积相等的了部分,你认为直线l是否存在?若存在求出直线l的表达式;若不存在,请说明理由
查看答案和解析>>
科目: 来源:2010年湖南湘潭市初中毕业学业考试数学试题 题型:059
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线y=ax2+bx+c过A、C、O三点.

(1)求点C的坐标和抛物线的解析式;
(2)过点B作直线与x轴交于点D,且OB2=OA·OD,求证:DB是⊙C的切线;
(3)抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为直角梯形,如果存在,求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com