
科目: 来源: 题型:解答题
如图,⊙M与x轴相切于点C,与y轴的一个交点为A。
(1)求证:AC平分∠OAM;
(2)如果⊙M的半径等于4,∠ACO=300,求AM所在直线的解析式.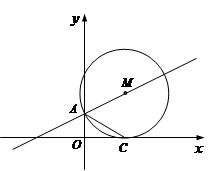
查看答案和解析>>
科目: 来源: 题型:解答题
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.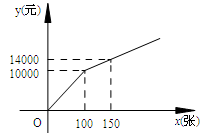
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知A(-4, )、B(2,-4)是一次函数
)、B(2,-4)是一次函数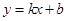 的图象和反比例函数
的图象和反比例函数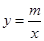 的图象的两个交点。
的图象的两个交点。
(1)求反比例函数和一次函数的解析式;
(2)求直线AB和 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;
(3)求方程 的解(请直接写出答案);
的解(请直接写出答案);
(4)求不等式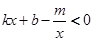 的解集(请直接写出答案)。
的解集(请直接写出答案)。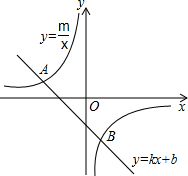
查看答案和解析>>
科目: 来源: 题型:解答题
平面直角坐标系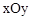 中,一次函数
中,一次函数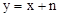 和反比例函数
和反比例函数 的图象都经过点
的图象都经过点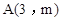 .
.
(1)求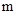 的值和一次函数的表达式;
的值和一次函数的表达式;
(2)点B在双曲线 上,且位于直线
上,且位于直线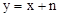 的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.
的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.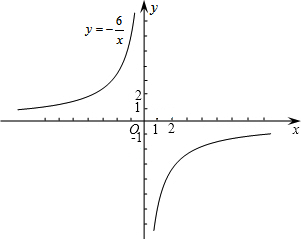
查看答案和解析>>
科目: 来源: 题型:解答题
在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
查看答案和解析>>
科目: 来源: 题型:解答题
已知:甲、乙两车分别从相距300千米的 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.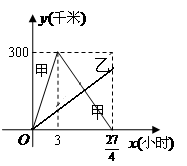
查看答案和解析>>
科目: 来源: 题型:解答题
在平面直角坐标系xOy中,一次函数y=- x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)求点P的坐标(用含t的代数式表示);
(2)当点Q从点O向点B运动时(未到达点B),是否存在实数t,使得△BPQ的面积大于17若存在,请求出t的取值范围;若不存在,请说明理由;
(3)伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.是否存在t的值,使得直线l经过点O?若存在,请求出所有t的值;若不存在,请说明理由.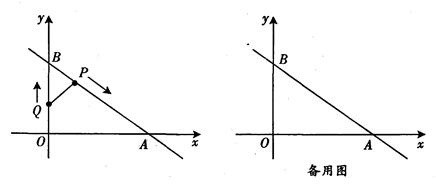
查看答案和解析>>
科目: 来源: 题型:解答题
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
查看答案和解析>>
科目: 来源: 题型:解答题
某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
“兄弟餐厅”采购员某日到集贸市场采购草鱼,若当天草鱼的采购单价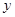 (元)与采购量
(元)与采购量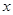 (斤)之间的关系如图,且采购单价不低于4元/斤.
(斤)之间的关系如图,且采购单价不低于4元/斤.
(1)直接写出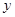 关于
关于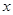 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)若这天他采购草鱼的量不多于20斤,那么这天他采购草鱼最多用去多少钱? 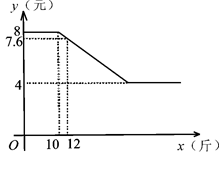
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com