
科目: 来源: 题型:解答题
如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.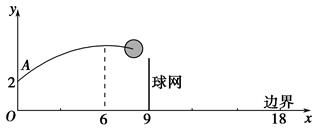
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.
(1)求抛物线的解析式;
(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+ (5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.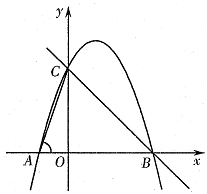
查看答案和解析>>
科目: 来源: 题型:解答题
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为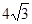 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.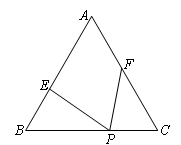
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)若经过B、E、C三点的抛物线的解析式为y=-x2+(2b-1)x+c-5,则b= ,c= (直接填空)
(2)①以P、D、E为顶点的三角形是直角三角形,则点P的坐标为 (直接填空)
②若抛物线顶点为N,又PE+PN的值最小时,求相应点P的坐标.
(3)连结QN,探究四边形PMNQ的形状:
①能否成为平行四边形
②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.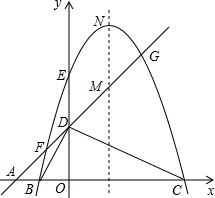
查看答案和解析>>
科目: 来源: 题型:解答题
某经销商代理销售一种手机,按协议,每卖出一部手机需另交品牌代理费100元,已知该种手机每部进价800元,销售单价为1200元时,每月能卖出100部,市场调查发现,若每部手机每让利50元,则每月可多售出40部.
(1)若每月要获取36000元利润,求让利价
(利润=销售收入-进货成本-品牌代理费)
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
查看答案和解析>>
科目: 来源: 题型:解答题
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.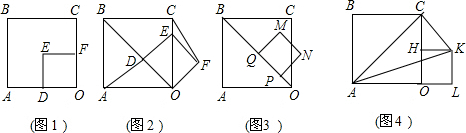
查看答案和解析>>
科目: 来源: 题型:解答题
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.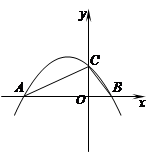
查看答案和解析>>
科目: 来源: 题型:解答题
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤ ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.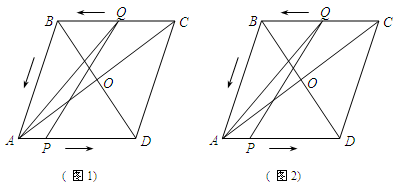
查看答案和解析>>
科目: 来源: 题型:解答题
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.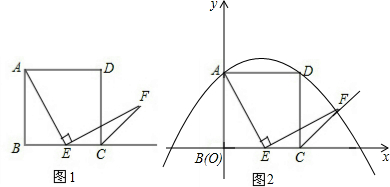
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com